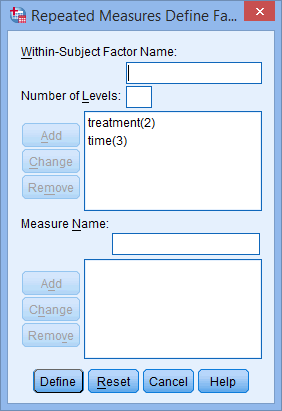
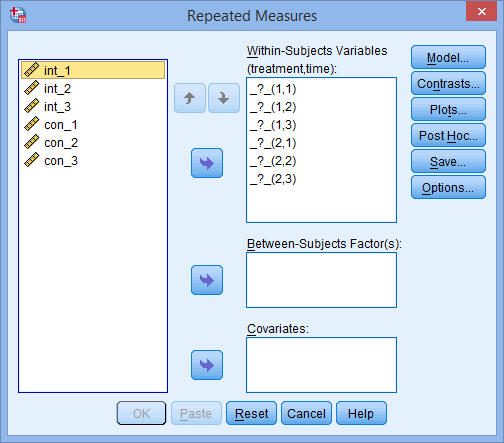
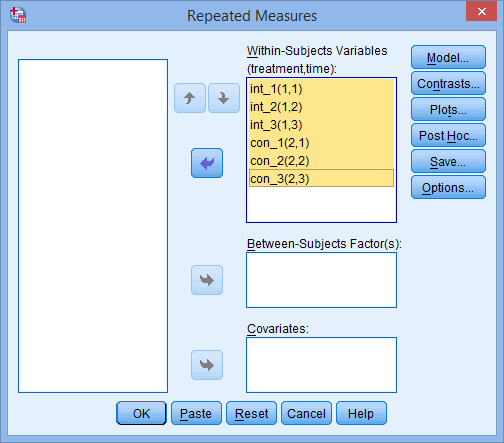
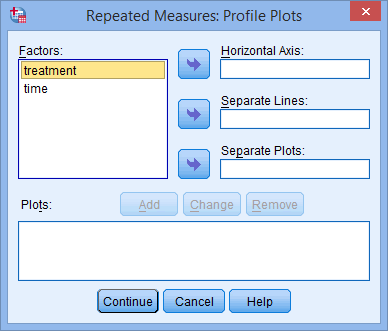
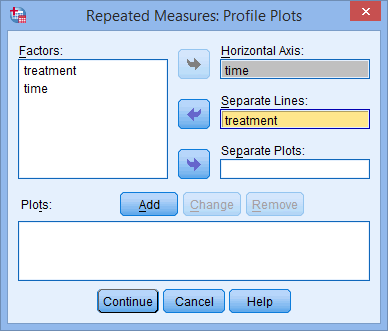
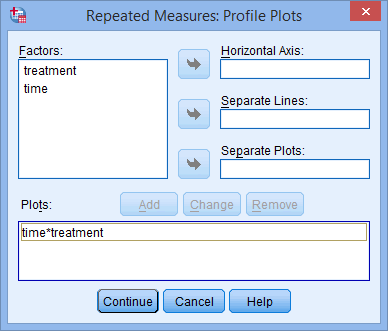
Two-way repeated measures ANOVA using SPSS Statistics

Introduction

A two-way repeated measures ANOVA (also known as a two-factor repeated measures ANOVA, two-factor or two-way ANOVA with repeated measures, or within-within-subjects ANOVA) compares the mean differences between groups that have been split on two within-subjects factors (also known as independent variables). A two-way repeated measures ANOVA is often used in studies where you have measured a dependent variable over two or more time points, or when subjects have undergone two or more conditions (i.e., the two factors are "time" and "conditions"). The primary purpose of a two-way repeated measures ANOVA is to understand if there is an interaction between these two factors on the dependent variable. Take a look at the examples below:

Once you have established whether there is a statistically significant interaction, there are a number of different approaches to following up the result. In particular, it is important to realize that the two-way repeated measures ANOVA is an omnibus test statistic and cannot tell you which specific groups within each factor were significantly different from each other. For example, if one of your factors (e.g., "time") has three groups (e.g., the three groups are your three time points: "time point 1", "time point 2" and "time point 3"), the two-way repeated measures ANOVA result cannot tell you whether the values on the dependent variable were different for one group (e.g., "Time point 1") compared with another group (e.g., "Time point 2"). It only tells you that at least two of the groups were different. Since you may have three, four, five or more groups in your study design, as well as two factors, determining which of these groups differ from each other is important. You can do this using post hoc tests, which we discuss later in this guide. In addition, where statistically significant interactions are found, you need to determine whether there are any "simple main effects", and if there are, what these effects are (again, we discuss later in our guide).

If you are unsure whether a two-way repeated measures ANOVA is appropriate, you may also want to consider how it differs from a one-way repeated measures ANOVA and a mixed ANOVA. A two-way repeated measures ANOVA goes further than a one-way repeated measures ANOVA, which only has one factor (i.e., one independent variable). For example, a one-way repeated measures ANOVA could be used when you only wanted to know whether there was a difference in chronic back pain before and after a back rehabilitation course (i.e., you only have one factor, which is "time", where you are comparing two groups, namely the two time points: "before" and "after" the back rehabilitation course). You should also distinguish between the two-way repeated measures ANOVA and the mixed ANOVA. A mixed ANOVA is very similar to a two-way repeated measures ANOVA because both of these statistical tests involve two factors (often "time" and some kind of "condition"), as well as a desire to understand whether there is an interaction between these two factors on the dependent variable. However, the fundamental difference is that in a mixed ANOVA, the subjects that undergo each condition (e.g., a control and treatment) are different, whereas in a two-way repeated measures ANOVA, the subjects undergo both conditions (e.g., they undergo the control and the treatment). Therefore, if you think that the two-way repeated measures ANOVA is not the test you are looking for, you may want to consider a one-way repeated measures ANOVA or mixed ANOVA. Alternately, if neither of these are appropriate, you can use our Statistical Test Selector, which is part of our enhanced content, to determine which test is appropriate for your study design.

In this "quick start" guide, we show you how to carry out a two-way repeated measures ANOVA with post hoc tests using SPSS Statistics, as well as the steps you will need to go through to interpret the results from this test. However, before we introduce you to this procedure, you need to understand the different assumptions that your data must meet in order for a two-way repeated measures ANOVA to give you a valid result. We discuss these assumptions next.

SPSS Statistics

Assumptions

When you choose to analyse your data using a two-way repeated measures ANOVA, part of the process involves checking to make sure that the data you want to analyse can actually be analysed using a two-way repeated measures ANOVA. You need to do this because it is only appropriate to use a two-way repeated measures ANOVA if your data "passes" five assumptions that are required for a two-way repeated measures ANOVA to give you a valid result. In practice, checking for these assumptions requires you to use SPSS Statistics to carry out a few more tests, as well as think a little bit more about your data, but it is not a difficult task.

Before we introduce you to these five assumptions, do not be surprised if, when analysing your own data using SPSS Statistics, one or more of these assumptions is violated (i.e., not met). This is not uncommon when working with real-world data rather than textbook examples. However, even when your data fails certain assumptions, there is often a solution to try and overcome this. First, let’s take a look at these five assumptions:

• Assumption #1: Your dependent variable should be measured at the continuous level (i.e., they are interval or ratio variables). Examples of continuous variables include revision time (measured in hours), intelligence (measured using IQ score), exam performance (measured from 0 to 100), weight (measured in kg), and so forth. You can learn more about interval and ratio variables in our article: Types of Variable.
• Assumption #2: Your two within-subjects factors (i.e., two independent variables) should consist of at least two categorical, "related groups" or "matched pairs". "Related groups" indicates that the same subjects are present in both groups. The reason that it is possible to have the same subjects in each group is because each subject has been measured on two occasions on the same dependent variable. For example, you might have measured 10 individuals' performance in a spelling test (the dependent variable) before and after they underwent a new form of computerized teaching method to improve spelling. You would like to know if the computer training improved their spelling performance. The first related group consists of the subjects at the beginning (prior to) the computerized spelling training and the second related group consists of the same subjects, but now at the end of the computerized training. The two-way repeated measures ANOVA can also be used to compare different subjects, but this does not happen very often. Nonetheless, to learn more about the different study designs you use with a two-way repeated measures ANOVA, see our enhanced two-way repeated measures ANOVA guide.
• Assumption #3: There should be no significant outliers in any combination of the related groups. Outliers are simply single data points within your data that do not follow the usual pattern (e.g., in a study of 100 students' IQ scores, where the mean score was 108 with only a small variation between students, one student had a score of 156, which is very unusual, and may even put her in the top 1% of IQ scores globally). The problem with outliers is that they can have a negative effect on the two-way repeated measures ANOVA, distorting the differences between the related groups (whether increasing or decreasing the scores on the dependent variable), which reduces the accuracy of your results. Fortunately, when using SPSS Statistics to run a two-way repeated measures ANOVA on your data, you can easily detect possible outliers. In our enhanced two-way repeated measures ANOVA guide, we: (a) show you how to detect outliers using SPSS Statistics; and (b) discuss some of the options you have in order to deal with outliers.
• Assumption #4: The distribution of the dependent variable in each combination of the related groups should be approximately normally distributed. We talk about the two-way repeated measures ANOVA only requiring approximately normal data because it is quite "robust" to violations of normality, meaning that assumption can be a little violated and still provide valid results. You can test for normality using the Shapiro-Wilk test of normality (using residuals), which is easily tested for using SPSS Statistics. In addition to showing you how to do this in our enhanced two-way repeated measures ANOVA guide, we also explain what you can do if your data fails this assumption (i.e., if it fails it more than a little bit).
• Assumption #5: Known as sphericity, the variances of the differences between all combinations of related groups must be equal. Fortunately, SPSS Statistics makes it easy to test whether your data has met or failed this assumption. Therefore, in our enhanced two-way repeated measures ANOVA guide, we (a) show you how to perform Mauchly's Test of Sphericity in SPSS Statistics, (b) explain some of the things you will need to consider when interpreting your data, and (c) present possible ways to continue with your analysis if your data fails to meet this assumption.

You can check assumptions #3, #4 and #5 using SPSS Statistics. Just remember that if you do not run the statistical tests on these assumptions correctly, the results you get when running a two-way repeated measures ANOVA might not be valid. This is why we dedicate a number of sections in our enhanced guides to help you get this right. You can find out about our enhanced content as a whole on our Features: Overview page, or more specifically, learn how we help with testing assumptions on our Features: Assumptions page.

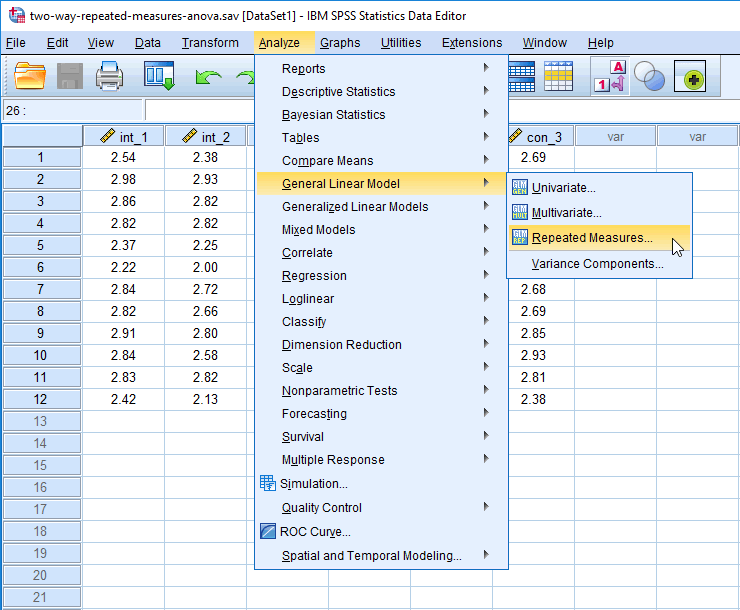
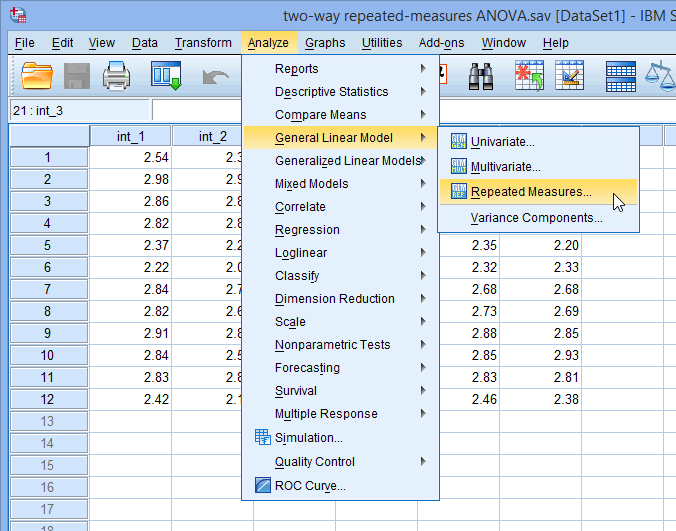
In the section, Procedure, we illustrate the SPSS Statistics procedure that you can use to carry out a two-way repeated measures ANOVA on your data. First, we introduce the example that is used in this guide.