Two-way ANCOVA in SPSS Statistics

Introduction

The two-way ANCOVA (also referred to as a "factorial ANCOVA") is used to determine whether there is an interaction effect between two independent variables in terms of a continuous dependent variable (i.e., if a two-way interaction effect exists), after adjusting/controlling for one or more continuous covariates. In many ways, the two-way ANCOVA can be considered an extension of the one-way ANCOVA, which has just one independent variable (rather than two independent variables), or an extension of the two-way ANOVA to incorporate one or more continuous covariates.

A two-way ANCOVA can be used in a number of situations. For example, consider an experiment where two drugs were being given to elderly patients to treat heart disease. One of the drugs was the current drug being used to treat heart disease and the other was an experimental drug that the researchers wanted to compare against the current drug. The researchers also wanted to understand how the drugs compared in low and high risk elderly patients. The goal was for the drugs to lower cholesterol concentration in the blood. The patients were of varying ages and the researchers wanted to control for these differences in age. Therefore, in this experiment the two independent variables are drug (with two groups: "Current" and "Experimental") and risk (with two levels: "Low" and "High"), the dependent variable was cholesterol (i.e., cholesterol concentration in the blood) and the continuous covariate was age. The researchers wanted to know: (a) whether the experimental drug was better or worse than the current drug at lowering cholesterol; and (b) whether the effect of the two drugs was different depending on whether elderly patients are classified as at low risk or high risk. These two aims are entirely typical of a two-way ANCOVA analysis. Importantly, the second aim is answered by determining whether there is a statistically significant two-way interaction effect. This is usually given first priority in a two-way ANCOVA analysis because its result will determine whether the researchers' first aim is misleading or incomplete. Assuming that a statistically significant two-way interaction effect is found, this indicates that the two drugs have different effects in low and high risk elderly patients (i.e., the effect of drug on cholesterol depends on level of risk), after adjusting/controlling for age. Depending on whether you find a statistically significant two-way interaction effect, and the type of interaction you have, will determine which effects in the two-way ANCOVA you should interpret and any post hoc tests you may want to run (i.e., where "post hoc tests" are follow-up analyses that are carried out after running a two-way ANCOVA analysis to learn more about your results).

In this introductory guide to the two-way ANCOVA, we first set out a couple of study designs where the two-way ANCOVA is most often used. Next, we set out the assumptions of the two-way ANCOVA. Making sure that your study design, variables and data pass these assumptions is critical because if they do not, the two-way ANCOVA is likely to be the incorrect statistical test to use. On page 2 of this introductory guide, we set out the example we use to illustrate the two-way ANCOVA using SPSS Statistics, before showing how to set up your data in the Variable View and Data View of SPSS Statistics. We then demonstrate the SPSS Statistics procedure to carry out a two-way ANCOVA using SPSS Statistics versions 25, 26 and 27 (and the subscription version of SPSS Statistics), with version 27 and the subscription version being the latest versions of the software, followed by version 24 and earlier versions of SPSS Statistics, since the procedure is slightly different in earlier versions of SPSS Statistics. If you are unsure which version of SPSS Statistics you are using, see our guide: Identifying your version of SPSS Statistics. Finally, on page 3 of this introductory guide, we explain how to interpret the main results of the two-way ANCOVA where you will determine if you have a statistically significant two-way interaction between your two independent variables in terms of your dependent variable (after adjusting for your covariate). Alternatively, if you would like to access our more comprehensive 28 page two-way ANCOVA guide, you can do so by subscribing to Laerd Statistics (please note that membership includes access to all of our guides). To continue with this introductory guide, go to the next section.

SPSS Statistics

Study Designs

The two-way ANCOVA can be used to analyse the results from a wide range of study designs, but it is broadly used for two types of study design: (a) an observational study; and (b) an experimental study. We explain both types of study design below:

OBSERVATIONAL STUDIES
The effect of test anxiety levels and gender on exam performance, controlling for revision time

The two-way ANCOVA can be used when you have an observational study design. In this type of study design, the researcher is placing participants into different groups of two independent variables based on the characteristics of those different groups. The researcher wants to know if there is an interaction effect between the two independent variables in terms of a continuous dependent variable (i.e., if a two-way interaction effect exists). One or more continuous covariates are used to statistically control other independent variables that are thought to influence this interaction effect (i.e., these other independent variables are called covariates). If there is a statistically significant interaction effect, this indicates that the effect that one independent variable has on the dependent variable depends on the level of the other independent variable, after controlling for the continuous covariate(s).

For example, imagine that a researcher wanted to determine whether there was a two-way interaction effect between gender and test anxiety levels in terms of exam performance, after controlling for revision time. Here, the continuous dependent variable is "exam performance" (measured from 0-100), the two categorical independent variables are "gender" (with two groups: "males" and "females") and "test anxiety levels" (with three levels: "low-stressed students", "moderately-stressed students" and "highly-stressed students"), and the continuous covariate is "revision time" (measured in hours).

Therefore, 90 male students and 90 female students were given a questionnaire to determine their level of test anxiety. Based on the results from this questionnaire, 23 students were classified as "low-stressed", 96 students were classified as "moderately-stressed", and 61 students were classified as "highly-stressed". No student could be in more than one of the three groups (e.g., a student that was classified as "highly-stressed" could not also be in the "moderately-stressed" group). Next, the exam marks of the 180 students were recorded. Finally, the amount of time each student spent revising was recorded.

A two-way ANCOVA was used to determine if there was a statistically significant two-way interaction effect between gender and test anxiety levels in terms of exam performance, after adjusting for the amount of time students' spent revising. If there was a two-way interaction effect, this would indicate that the effect that one independent variable (e.g., gender) had on the dependent variable (e.g., exam performance) depended on the level of the other independent variable (e.g., test anxiety levels), whilst controlling for the continuous covariate (e.g., revision time). This analysis could then be followed-up using simple main effects or interaction contrasts to determine the effect that the different groups/levels of each independent variable had on the dependent variable, after controlling for the covariate. For example, it could tell us whether exam performance, after adjusting for revision time, was lower for highly-stressed males students than highly-stressed female students. Depending on the type of interaction between the two independent variables, it is possible to also carry out main effects analysis. Alternatively, if there was no interaction effect, the analysis could be followed-up using main effects (and even simple main effects in some cases, depending on the type of interaction between the two independent variables).

EXPERIMENTAL STUDIES
The effect of different drug types and treatment programmes on cholesterol concentration, controlling for weight

The two-way ANCOVA can be used when you have an experimental study design. In this type of study design, the researcher is manipulating the two independent variables so that different participants are receiving different interventions/conditions. The researcher wants to know if there is an interaction effect between the two independent variables in terms of a continuous dependent variable (i.e., if a two-way interaction effect exists). One or more continuous covariates are used to statistically control for other independent variables that are thought to influence this interaction effect (i.e., these other independent variables are called covariates). If there is a statistically significant two-way interaction effect, this indicates that the effect that one independent variable has on the dependent variable depends on the level of the other independent variable, after controlling for the continuous covariate(s).

For example, imagine that a researcher wanted to determine whether there was a two-way interaction effect between different types of drug and treatment programme in terms of cholesterol concentration, after controlling for weight. Here, the continuous dependent variable is "cholesterol concentration" in the blood (measured in mmol/L), the two categorical independent variables are "drug type" (with three groups: "Drug A", "Drug B" and "Drug C") and "treatment programme" (with three groups: "Control group", "Exercise programme" and "Diet programme"), and the continuous covariate is "weight" (measured in kg).

Therefore, 225 participants were recruited and were randomly assigned to one of the nine groups: (1) "Drug A" and the "Control group"; (2) "Drug B" and the "Control group"; (3) "Drug C" and the "Control group"; (4) "Drug A" and the "Exercise programme"; (5) "Drug B" and the "Exercise programme"; (6) "Drug C" and the "Exercise programme"; (7) "Drug A" and the "Diet programme"; (8) "Drug B" and the "Diet programme"; (9) "Drug C" and the "Diet programme". Therefore, Group 1 was given "Drug A" and were in the "Control group", meaning that they did not undergo any treatment/intervention. Also, there was an equal number of participants in each of the nine groups (i.e., 25 participants). No participant could be in more than one of the nine groups. The weight of all 225 participants was recorded before any treatment/intervention took place. At the end of the experiment (i.e., after the 6-month exercise and diet programmes), the cholesterol concentration of all 225 participants was recorded.

A two-way ANCOVA was used to determine if there was a statistically significant two-way interaction effect between drug type and treatment programme in terms of cholesterol concentration, after adjusting for participants' weight. If there was a two-way interaction effect, this would indicate that the effect that one independent variable (e.g., drug type) had on the dependent variable (e.g., cholesterol concentration) depended on the level of the other independent variable (e.g., treatment programme), whilst controlling for the continuous covariate (e.g., weight). This analysis could then be followed-up using simple main effects or interaction contrasts to determine the effect that the different groups/levels of each independent variable had on the dependent variable, after controlling for the covariate. For example, it could tell us whether cholesterol concentration, after adjusting for participants' weight, was lower for participants who took drug A and exercised compared to participants who took drug A and did not exercise (i.e., those who did nothing and were in the control group, or those who underwent the diet programme instead of exercising). Depending on the type of interaction between the two independent variables, it is possible to also carry out main effects analysis. Alternatively, if there was no interaction effect, the analysis could be followed-up using main effects (and even simple main effects in some cases, depending on the type of interaction between the two independent variables).

Now that you have an idea of the types of study design where the two-way ANCOVA is used, we recommend reading about the assumptions of the two-way ANCOVA in the next section.

SPSS Statistics

Assumptions

When you choose to analyse your data using a two-way ANCOVA, a critical part of the process involves checking to make sure that the data you want to analyse can actually be analysed using a two-way ANCOVA. You need to do this because it is only appropriate to use a two-way ANCOVA if your data "passes" 10 assumptions that are required for a two-way ANCOVA to give you a valid result. Before we introduce you to these 10 assumptions, do not be surprised if, when analysing your own data using SPSS Statistics, one or more of these assumptions is violated (i.e., is not met). This is not uncommon when working with real-world data rather than textbook examples, which often only show you how to carry out a two-way ANCOVA when everything goes well! However, don’t worry. Even when your data fails certain assumptions, there is often a solution to overcome this.

For the two-way ANCOVA, four of the 10 assumptions relate to how you measured your variables and your study design, which can be checked before you carry out any analysis. We suggest that you do this first because if your variables and study design do not fit a two-way ANCOVA analysis, you will not need to read the remainder of this introductory guide! Therefore, these four assumptions are set out below:

• Assumption #1: Your dependent variable should be measured at the continuous level (i.e., it is an interval or ratio variable). Examples of continuous variables include revision time (measured in hours), intelligence (measured using IQ score), exam performance (measured from 0 to 100) and weight (measured in kg). You can learn more about interval and ratio variables in our guide: Types of Variable.

  Important: If your dependent variable is not measured on a continuous scale, but is either a count variable, ordinal variable, nominal variable or dichotomous variable, the two-way ANCOVA would not be an appropriate statistical test. Again, if you are unsure about these different types of variable, please see our guide: Types of Variable. If you have this scenario and are unsure of the appropriate statistical test, we have a Statistical Test Selector within the members part of Laerd Statistics, which you can access by subscribing to our site.

• Assumption #2: Your two independent variables should each consist of two or more categorical, independent groups. Categorical variables include both nominal variables and ordinal variables. Examples of nominal variables include gender (two groups: male or female) and ethnicity (three groups: Caucasian, African American and Hispanic) and profession (four groups: surgeon, doctor, nurse and dentist). Examples of ordinal variables include BMI (two levels: "normal" and "obese"), physical activity level (four levels: "sedentary", "low", "moderate" and "high"), Likert items (e.g., a 7-point scale from "strongly agree" through to "strongly disagree"), amongst other ways of ranking categories (e.g., a 3-point scale explaining how much a customer liked a product, ranging from "Not very much", to "It is OK", to "Yes, a lot").

  Note 1: It is quite common for the independent variables to be called "factors" or "between-subjects factors", but we will continue to refer to them as independent variables. Furthermore, the two-way ANCOVA is also referred to as a "factorial ANCOVA" because ANCOVAs with two or more independent variables are all classified as factorial ANCOVAs.

  Note 2: A two-way ANCOVA can be described by the number of groups in each independent variable. For example, if you had a two-way ANCOVA with "gender" (2 groups: "male" and "female") and "transport type" (3 groups: "bus", "train" and "car") as the independent variables, and salary as a covariate, you could describe this as a 2 x 3 ANCOVA. This is a fairly generic way to describe ANCOVAs.

• Assumption #3: Your one or more covariates, also known as control variables, are all continuous variables (see Assumption #1 for examples of continuous variables). A covariate is simply a continuous independent variable that is added to an ANOVA model to produce an ANCOVA model. This covariate is used to adjust the means of the groups of the two categorical independent variables. In an ANCOVA the covariate is generally only there to provide a better assessment of the differences between the groups of the categorical independent variables in terms of the dependent variable. To illustrate this, in our example above of two drugs that were being tested to determine how they affected cholesterol concentration (a marker of heart disease) in low and high risk elderly patients, the researcher used "age" as a covariate to control for the different ages of participants in the study (e.g., cholesterol concentration is generally higher with age so controlling for age would help to improve the likelihood of finding a statistically significant two-way interaction effect if one exists).

  Note: It is possible to carry out a two-way ANCOVA when your covariates are categorical variables (i.e., nominal variables or ordinal variables) or a mix of categorical and continuous variables. However, this involves some extra steps when testing the assumptions of the two-way ANCOVA, as well as some differences in the SPSS Statistics procedure to carry out a two-way ANCOVA, and how you will interpret some of your results. We do not show how to deal with categorical covariates in this introductory guide, or the enhanced guide within the members section of Laerd Statistics, but will be adding a guide to help. If you would like to know when we add this guide, please contact us.

• Assumption #4: You should have independence of observations, which means that there is no relationship between the observations in each group or between the groups themselves. For example, there must be different participants in each group with no participant being in more than one group. This is more of a study design issue than something you would test for, but it is an important assumption of the two-way ANCOVA. If your study fails this assumption, you will need to use another statistical test instead of the two-way ANCOVA (e.g., a repeated measures design). If you are unsure whether your study meets this assumption, you can use our Statistical Test Selector within the members' part of Laerd Statistics, which you can access by subscribing to our site.

If your data meets these first four assumptions, the two-way ANCOVA might be an appropriate statistical test to analyse your data. To determine whether it is the correct statistical test, you now need to test whether your data "passes" a further six assumptions. In practice, this is the most time consuming and tricky part of a two-way ANCOVA analysis. You will have to carry out multiple procedures in SPSS Statistics and interpret the results from these procedures to check if your data passes each of these six assumptions. As we mentioned before, do not be surprised if, when analysing your own data using SPSS Statistics, one or more of these assumptions is violated (i.e., is not met). This is not uncommon when working with real-world data, but there are often solutions to overcome such problems.

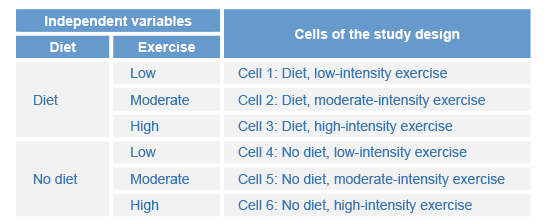
• Assumption #5: The covariate should be linearly related to the dependent variable for each combination of groups of the independent variables (i.e., each cell of the design). When we refer to each cell of the design or each combination of groups of the independent variables, consider the following example where the independent variable, "diet", has two groups and the independent variable, "exercise", has three levels:
  
  
  
  In this example there are six cells in the design (i.e., 2 groups x 3 levels = 6 cells of the design). You can test this assumption in SPSS Statistics by plotting a grouped scatterplot and adding loess lines to make the interpretation easier.
• Assumption #6: There should be homogeneity of regression slopes. This assumption checks that the relationship between the covariate and the dependent variable, as assessed by the regression slope, is the same in each cell of the design (i.e., for each combination of groups of the two independent variables). Simply put, the previous assumption assessed whether the relationships were linear; this assumption now checks whether these linear relationships are the same. This assumption can also be tested in SPSS Statistics, but it requires quite a few steps, including using the Compute Variable and Univariate procedures in SPSS Statistics.
• Assumption #7: There should be homoscedasticity. An important assumption of the two-way ANCOVA is that the variance of the error is identical for all combinations of the values of the independent variables and covariate. This can be tested in two parts, one of which can be referred to as testing for homoscedasticity; that is, there should be homoscedasticity of error variances within each combination of groups of the two independent variables (i.e., within each cell of the design) (Huitema, 2011). Homoscedasticity can be checked in SPSS Statistics by inspecting a plot of the studentized residuals against the predicted values for each cell of the design (i.e., each combination of groups of the independent variables).
• Assumption #8: There should be homogeneity of variances. To reiterate from Assumption #7 above, an important assumption of the two-way ANCOVA is that the variance of the error is identical for all combinations of the values of the independent variables and covariate. The second part to testing this assumption is referred to as testing for homogeneity of variances; that is, the variances of the residuals should be equal between each combination of groups of the two independent variables (i.e., between each cell of the design) (Huitema, 2011). If the variances are unequal, this can affect the Type I error rate. This can be tested in SPSS Statistics using Levene's test of equality of variances.
• Assumption #9: There should be no significant unusual points in any combinations of groups of your two independent variables. There can be certain data points that are, in some way, classified as unusual from the perspective of fitting a two-way ANCOVA model. These data points are generally detrimental to the fit or generalization (statistical inference) of the two-way ANCOVA. There are three main types of unusual point: outliers, leverage points and influential points. An observation can be classified as more than one type of unusual point. Whilst all are unusual, these different classifications of unusual point reflect the different impact they have on the two-way ANCOVA model. For example, you can have observations in your data set that have an unusual combination of values on the independent variables (i.e., leverage points) or affect the parameter estimates of the two-way ANCOVA in a detrimental manner (i.e., influential points). You can check for unusual points in SPSS Statistics by inspecting the values of the studentized residuals, the leverage values and Cook's distance values.
• Assumption #10: Your residuals should be approximately normally distributed for each combination of groups of the two independent variables. There are many different methods available to test this assumption, including numerical methods such as the Shapiro-Wilk test for normality, as well as graphical methods such as normal Q-Q plots.

You can check assumptions #5, #6, #7, #8, #9 and #10 using SPSS Statistics. Before doing this, you should make sure that your data meets assumptions #1, #2, #3 and #4, although you don’t need SPSS Statistics to do this. Just remember that if you do not run the statistical tests on these assumptions correctly, the results you get when running a two-way ANCOVA might be incorrect. If you are unsure how to test assumptions #5, #6, #7, #8, #9 and #10 using SPSS Statistics, we dedicate 9 of our 28 page guide on the two-way ANCOVA to help with this (N.B., you can access this more comprehensive 28 page guide by subscribing to Laerd Statistics). To continue with this introductory guide, go to the next page where we start by setting out the example we use to illustrate the two-way ANCOVA using SPSS Statistics.