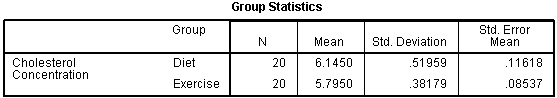Independent t-test using SPSS Statistics
Introduction
The independent-samples t-test (or independent t-test, for short) compares the means between two unrelated groups on the same continuous, dependent variable. For example, you could use an independent t-test to understand whether first year graduate salaries differed based on gender (i.e., your dependent variable would be "first year graduate salaries" and your independent variable would be "gender", which has two groups: "male" and "female"). Alternately, you could use an independent t-test to understand whether there is a difference in test anxiety based on educational level (i.e., your dependent variable would be "test anxiety" and your independent variable would be "educational level", which has two groups: "undergraduates" and "postgraduates").
This "quick start" guide shows you how to carry out an independent t-test using SPSS Statistics, as well as interpret and report the results from this test. However, before we introduce you to this procedure, you need to understand the different assumptions that your data must meet in order for an independent t-test to give you a valid result. We discuss these assumptions next.
SPSS Statistics
Assumptions
When you choose to analyse your data using an independent t-test, part of the process involves checking to make sure that the data you want to analyse can actually be analysed using an independent t-test. You need to do this because it is only appropriate to use an independent t-test if your data "passes" six assumptions that are required for an independent t-test to give you a valid result. In practice, checking for these six assumptions just adds a little bit more time to your analysis, requiring you to click a few more buttons in SPSS Statistics when performing your analysis, as well as think a little bit more about your data, but it is not a difficult task.
Before we introduce you to these six assumptions, do not be surprised if, when analysing your own data using SPSS Statistics, one or more of these assumptions is violated (i.e., is not met). This is not uncommon when working with real-world data rather than textbook examples, which often only show you how to carry out an independent t-test when everything goes well! However, don't worry. Even when your data fails certain assumptions, there is often a solution to overcome this. First, let's take a look at these six assumptions:
- Assumption #1: Your dependent variable should be measured on a continuous scale (i.e., it is measured at the interval or ratio level). Examples of variables that meet this criterion include revision time (measured in hours), intelligence (measured using IQ score), exam performance (measured from 0 to 100), weight (measured in kg), and so forth. You can learn more about continuous variables in our article: Types of Variable.
- Assumption #2: Your independent variable should consist of two categorical, independent groups. Example independent variables that meet this criterion include gender (2 groups: male or female), employment status (2 groups: employed or unemployed), smoker (2 groups: yes or no), and so forth.
- Assumption #3: You should have independence of observations, which means that there is no relationship between the observations in each group or between the groups themselves. For example, there must be different participants in each group with no participant being in more than one group. This is more of a study design issue than something you can test for, but it is an important assumption of the independent t-test. If your study fails this assumption, you will need to use another statistical test instead of the independent t-test (e.g., a paired-samples t-test). If you are unsure whether your study meets this assumption, you can use our Statistical Test Selector, which is part of our enhanced content.
- Assumption #4: There should be no significant outliers. Outliers are simply single data points within your data that do not follow the usual pattern (e.g., in a study of 100 students' IQ scores, where the mean score was 108 with only a small variation between students, one student had a score of 156, which is very unusual, and may even put her in the top 1% of IQ scores globally). The problem with outliers is that they can have a negative effect on the independent t-test, reducing the validity of your results. Fortunately, when using SPSS Statistics to run an independent t-test on your data, you can easily detect possible outliers. In our enhanced independent t-test guide, we: (a) show you how to detect outliers using SPSS Statistics; and (b) discuss some of the options you have in order to deal with outliers. You can learn more about our enhanced independent t-test guide here.
- Assumption #5: Your dependent variable should be approximately normally distributed for each group of the independent variable. We talk about the independent t-test only requiring approximately normal data because it is quite "robust" to violations of normality, meaning that this assumption can be a little violated and still provide valid results. You can test for normality using the Shapiro-Wilk test of normality, which is easily tested for using SPSS Statistics. In addition to showing you how to do this in our enhanced independent t-test guide, we also explain what you can do if your data fails this assumption (i.e., if it fails it more than a little bit). Again, you can learn more here.
- Assumption #6: There needs to be homogeneity of variances. You can test this assumption in SPSS Statistics using Levene’s test for homogeneity of variances. In our enhanced independent t-test guide, we (a) show you how to perform Levene’s test for homogeneity of variances in SPSS Statistics, (b) explain some of the things you will need to consider when interpreting your data, and (c) present possible ways to continue with your analysis if your data fails to meet this assumption (learn more here).
You can check assumptions #4, #5 and #6 using SPSS Statistics. Before doing this, you should make sure that your data meets assumptions #1, #2 and #3, although you don't need SPSS Statistics to do this. When moving on to assumptions #4, #5 and #6, we suggest testing them in this order because it represents an order where, if a violation to the assumption is not correctable, you will no longer be able to use an independent t-test (although you may be able to run another statistical test on your data instead). Just remember that if you do not run the statistical tests on these assumptions correctly, the results you get when running an independent t-test might not be valid. This is why we dedicate a number of sections of our enhanced independent t-test guide to help you get this right. You can find out about our enhanced independent t-test guide here, or more generally, our enhanced content as a whole here.
In the section, Test Procedure in SPSS Statistics, we illustrate the SPSS Statistics procedure required to perform an independent t-test assuming that no assumptions have been violated. First, we set out the example we use to explain the independent t-test procedure in SPSS Statistics.
SPSS Statistics
Example
The concentration of cholesterol (a type of fat) in the blood is associated with the risk of developing heart disease, such that higher concentrations of cholesterol indicate a higher level of risk, and lower concentrations indicate a lower level of risk. If you lower the concentration of cholesterol in the blood, your risk of developing heart disease can be reduced. Being overweight and/or physically inactive increases the concentration of cholesterol in your blood. Both exercise and weight loss can reduce cholesterol concentration. However, it is not known whether exercise or weight loss is best for lowering cholesterol concentration. Therefore, a researcher decided to investigate whether an exercise or weight loss intervention is more effective in lowering cholesterol levels. To this end, the researcher recruited a random sample of inactive males that were classified as overweight. This sample was then randomly split into two groups: Group 1 underwent a calorie-controlled diet and Group 2 undertook the exercise-training programme. In order to determine which treatment programme was more effective, the mean cholesterol concentrations were compared between the two groups at the end of the treatment programmes.
SPSS Statistics
Setup in SPSS Statistics
In SPSS Statistics, we separated the groups for analysis by creating a grouping variable called Treatment (i.e., the independent variable), and gave the "diet group" a value of "1" and the "exercise group" a value of "2" (i.e., the two groups of the independent variable). Cholesterol concentrations were entered under the variable name Cholesterol (i.e., the dependent variable). In our enhanced independent t-test guide, we show you how to correctly enter data in SPSS Statistics to run an independent t-test (see here). You can learn about our enhanced data setup content in general here. Alternately, we have a generic, "quick start" guide to show you how to enter data into SPSS Statistics, available here.
SPSS Statistics
Test Procedure in SPSS Statistics
The eight steps below show you how to analyse your data using an independent t-test in SPSS Statistics when the six assumptions in the previous section, Assumptions, have not been violated. At the end of these eight steps, we show you how to interpret the results from this test. If you are looking for help to make sure your data meets assumptions #4, #5 and #6, which are required when using an independent t-test, and can be tested using SPSS Statistics, you can learn more here.
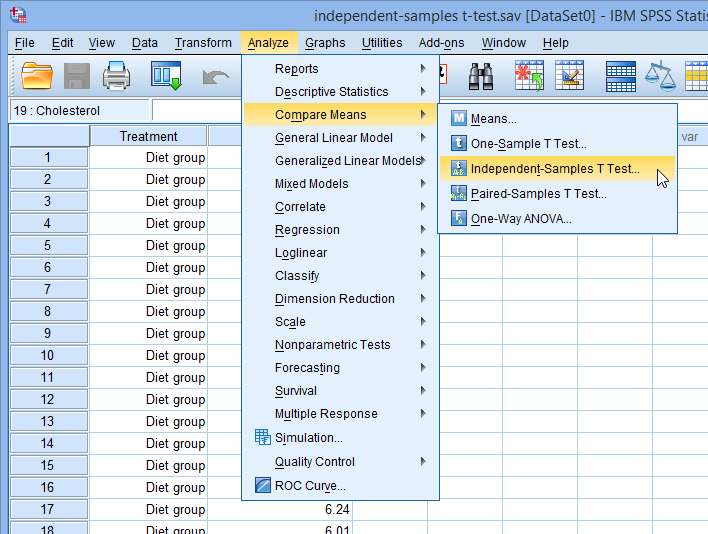
- Click Analyze > Compare Means > Independent-Samples T Test... on the top menu, as shown below:

Published with written permission from SPSS Statistics, IBM Corporation.
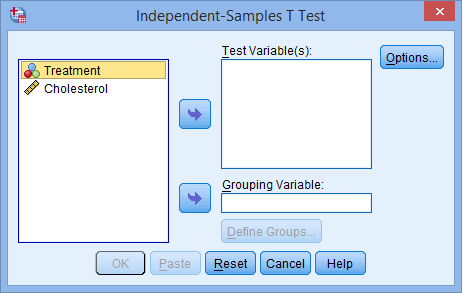
You will be presented with the Independent-Samples T Test dialogue box, as shown below:

Published with written permission from SPSS Statistics, IBM Corporation.
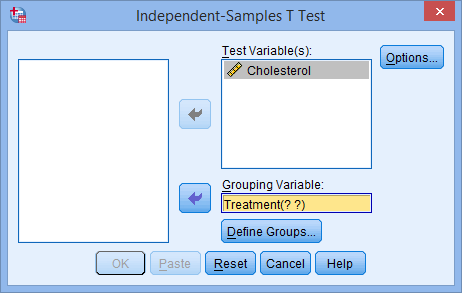
- Transfer the dependent variable, Cholesterol, into the Test Variable(s): box, and transfer the independent variable, Treatment, into the Grouping Variable: box, by highlighting the relevant variables and pressing the
 buttons. You will end up with the following screen:
buttons. You will end up with the following screen:
Published with written permission from SPSS Statistics, IBM Corporation.
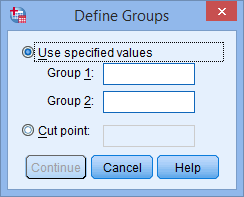
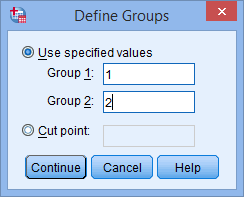
- You then need to define the groups (treatments). Click on the
 button. You will be presented with the Define Groups dialogue box, as shown below:
button. You will be presented with the Define Groups dialogue box, as shown below: 
Published with written permission from SPSS Statistics, IBM Corporation.
- Enter "1" into the Group 1: box and enter "2" into the Group 2: box. Remember that we labelled the Diet Treatment group as 1 and the Exercise Treatment group as 2.

Published with written permission from SPSS Statistics, IBM Corporation.
Note: If you have more than 2 treatment groups in your study (e.g., 3 groups: diet, exercise and drug treatment groups), but only wanted to compared two (e.g., the diet and drug treatment groups), you could type in 1 to Group 1: box and 3 to Group 2: box (i.e., if you wished to compare the diet with drug treatment).
- Click the
 button.
button. - If you need to change the confidence level limits or change how to exclude cases, click the
 button. You will be presented with the following:
button. You will be presented with the following:
Published with written permission from SPSS Statistics, IBM Corporation.
- Click the
 button. You will be returned to the Independent-Samples T Test dialogue box.
button. You will be returned to the Independent-Samples T Test dialogue box. - Click the
 button.
button.
SPSS Statistics
Output of the independent t-test in SPSS Statistics
SPSS Statistics generates two main tables of output for the independent t-test. If your data passed assumption #4 (i.e., there were no significant outliers), assumption #5 (i.e., your dependent variable was approximately normally distributed for each group of the independent variable) and assumption #6 (i.e., there was homogeneity of variances), which we explained earlier in the Assumptions section, you will only need to interpret these two main tables. However, since you should have tested your data for these assumptions, you will also need to interpret the SPSS Statistics output that was produced when you tested for them (i.e., you will have to interpret: (a) the boxplots you used to check if there were any significant outliers; (b) the output SPSS Statistics produces for your Shapiro-Wilk test of normality to determine normality; and (c) the output SPSS Statistics produces for Levene's test for homogeneity of variances). If you do not know how to do this, we show you in our enhanced independent t-test guide here. Remember that if your data failed any of these assumptions, the output that you get from the independent t-test procedure (i.e., the tables we discuss below) might not be valid and you might need to interpret these tables differently.
However, in this "quick start" guide, we take you through each of the two main tables in turn, assuming that your data met all the relevant assumptions.
Group Statistics Table
This table provides useful descriptive statistics for the two groups that you compared, including the mean and standard deviation.

Published with written permission from SPSS Statistics, IBM Corporation.
Unless you have other reasons to do so, it would be considered normal to present information on the mean and standard deviation for this data. You might also state the number of participants that you had in each of the two groups. This can be useful when you have missing values and the number of recruited participants is larger than the number of participants that could be analysed.
A diagram can also be used to visually present your results. For example, you could use a bar chart with error bars (e.g., where the error bars could use the standard deviation, standard error or 95% confidence intervals). This can make it easier for others to understand your results. Again, we show you how to do this in our enhanced independent t-test guide.
Independent Samples Test Table
This table provides the actual results from the independent t-test.

Published with written permission from SPSS Statistics, an IBM Corporation.
You can see that the group means are statistically significantly different because the value in the "Sig. (2-tailed)" row is less than 0.05. Looking at the Group Statistics table, we can see that those people who undertook the exercise trial had lower cholesterol levels at the end of the programme than those who underwent a calorie-controlled diet.
SPSS Statistics
Reporting the output of the independent t-test
Based on the results above, you could report the results of the study as follows (N.B., this does not include the results from your assumptions tests or effect size calculations):
This study found that overweight, physically inactive male participants had statistically significantly lower cholesterol concentrations (5.80 ± 0.38 mmol/L) at the end of an exercise-training programme compared to after a calorie-controlled diet (6.15 ± 0.52 mmol/L), t(38)=2.428, p=0.020.
In our enhanced independent t-test guide, we show you how to write up the results from your assumptions tests and independent t-test procedure if you need to report this in a dissertation, thesis, assignment or research report. We do this using the Harvard and APA styles (see here). It is also worth noting that in addition to reporting the results from your assumptions and independent t-test, you are increasingly expected to report effect sizes. Whilst there are many different ways you can do this, we show you how to calculate effect sizes from your SPSS Statistics results in our enhanced independent t-test guide. Effect sizes are important because whilst the independent t-test tells you whether differences between group means are "real" (i.e., different in the population), it does not tell you the "size" of the difference. Providing an effect size in your results helps to overcome this limitation. You can learn more about our enhanced independent t-test guide here, or our enhanced content in general here. If you use Stata rather than SPSS Statistics, we have a "quick start" guide on how to run an independent t-test here.