Standard Score (cont...)
Clearly, the two scores (her English Literature and Maths coursework marks) come from different distributions. The distribution of 50 students that completed the English Literature coursework has a mean of 60 and standard deviation of 15. The distribution of 50 students that completed the Maths coursework, on the other hand, has a mean of 68 and a standard deviation of 6. This gives us the following:
| Score | Mean | Standard Deviation | |
| (X) | µ | s | |
| English Literature | 70 | 60 | 15 |
| Maths | 72 | 68 | 6 |
Since these scores are from two different distributions, we need to standardise them into z-scores so that they can be directly compared. This gives us:
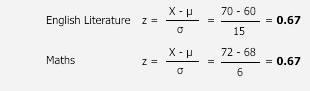
The z-scores highlight that the student is two thirds (z = 0.67) of a standard deviation above the mean in English Literature, but also two thirds (z = 0.67) of a standard deviation above the mean in Maths. Using the standard normal distribution table, we can see that Sarah clearly performed above 'average' in both subjects although again, around 25% of the class got a better mark than her. However, the key point her is that the standard score showed that Sarah performed equally well in her English Literature and Maths coursework, even though her marks were different in both pieces. This shows the usefulness of the standard score statistic.
In the following statistical guide, Hypothesis Testing, we start to set out some of the key aspects of quantitative research.