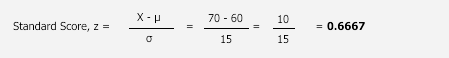Standard Score (cont...)
Z-scores are expressed in terms of standard deviations from their means. Resultantly, these z-scores have a distribution with a mean of 0 and a standard deviation of 1. The formula for calculating the standard score is given below:
As the formula shows, the standard score is simply the score, minus the mean score, divided by the standard deviation. Therefore, let's return to our two questions.
1. How well did Sarah perform in her English Literature coursework compared to the other 50 students?
To answer this question, we can re-phrase it as: What percentage (or number) of students scored higher than Sarah and what percentage (or number) of students scored lower than Sarah? First, let's reiterate that Sarah scored 70 out of 100, the mean score was 60, and the standard deviation was 15 (see below).
| |
Score |
Mean |
Standard Deviation |
| |
(X) |
µ |
s |
| English Literature |
70 |
60 |
15 |
In terms of z-scores, this gives us:
The z-score is 0.67 (to 2 decimal places), but now we need to work out the percentage (or number) of students that scored higher and lower than Sarah. To do this, we need to refer to the standard normal distribution table.
This table helps us to identify the probability that a score is greater or less than our z-score score. To use the table, which is easier than it might look at first sight, we start with our z-score, 0.67 (if our z-score had more than two decimal places, for example, ours was 0.6667, we would round it up or down accordingly; hence, 0.6667 would become 0.67). The y-axis in the table highlights the first two digits of our z-score and the x-axis the second decimal place. Therefore, we start with the y-axis, finding 0.6, and then move along the x-axis until we find 0.07, before finally reading off the appropriate number; in this case, 0.2514. This means that the probability of a score being greater than 0.67 is 0.2514. If we look at this as a percentage, we simply times the score by 100; hence 0.2514 x 100 = 25.14%. In other words, around 25% of the class got a better mark than Sarah (roughly 13 students since there is no such thing as part of a student!).
Going back to our question, "How well did Sarah perform in her English Literature coursework compared to the other 50 students?", clearly we can see that Sarah did better than a large proportion of students, with 74.86% of the class scoring lower than her (100% - 25.14% = 74.86%). We can also see how well she performed relative to the mean score by subtracting her score from the mean (0.5 - 0.2514 = 0.2486). Hence, 24.86% of the scores (0.2486 x 100 = 24.86%) were lower than Sarah's, but above the mean score. However, the key finding is that Sarah's score was not one of the best marks. It wasn't even in the top 10% of scores in the class, even though at first sight we may have expected it to be. This leads us onto the second question.
2. Which students came in the top 10% of the class?
A better way of phrasing this would be to ask: What mark would a student have to achieve to be in the top 10% of the class and qualify for the advanced English Literature class?