Login

One-way ANOVA

What is this test for?

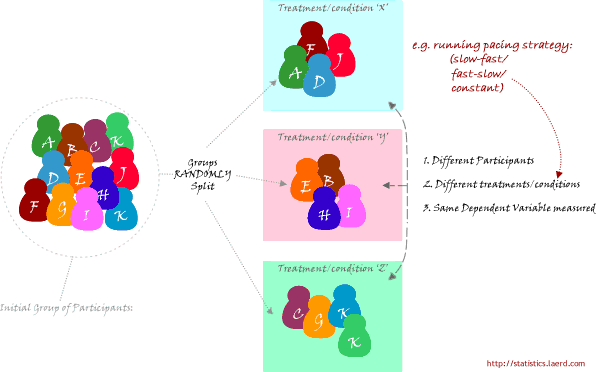
The one-way analysis of variance (ANOVA) is used to determine whether there are any statistically significant differences between the means of three or more independent (unrelated) groups. This guide will provide a brief introduction to the one-way ANOVA, including the assumptions of the test and when you should use this test. If you are familiar with the one-way ANOVA, but would like to carry out a one-way ANOVA analysis, go to our guide: One-way ANOVA in SPSS Statistics.

What does this test do?

The one-way ANOVA compares the means between the groups you are interested in and determines whether any of those means are statistically significantly different from each other. Specifically, it tests the null hypothesis:

One-way ANOVA Null Hypothesis

where µ = group mean and k = number of groups. If, however, the one-way ANOVA returns a statistically significant result, we accept the alternative hypothesis (HA), which is that there are at least two group means that are statistically significantly different from each other.

At this point, it is important to realize that the one-way ANOVA is an omnibus test statistic and cannot tell you which specific groups were statistically significantly different from each other, only that at least two groups were. To determine which specific groups differed from each other, you need to use a post hoc test. Post hoc tests are described later in this guide.

Join the 10,000s of students, academics and professionals who rely on Laerd Statistics.TAKE THE TOUR

When might you need to use this test?

If you are dealing with individuals, you are likely to encounter this situation using two different types of study design:

One study design is to recruit a group of individuals and then randomly split this group into three or more smaller groups (i.e., each participant is allocated to one, and only one, group). You then get each group to undertake different tasks (or put them under different conditions) and measure the outcome/response on the same dependent variable. For example, a researcher wishes to know whether different pacing strategies affect the time to complete a marathon. The researcher randomly assigns a group of volunteers to either a group that (a) starts slow and then increases their speed, (b) starts fast and slows down or (c) runs at a steady pace throughout. The time to complete the marathon is the outcome (dependent) variable. This study design is illustrated schematically in the diagram below:

One-way ANOVA - Design 1

When you might use this test is continued on the next page.

1 234
next »