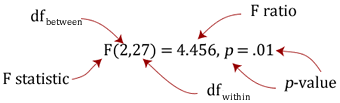Login

One-way ANOVA (cont...)

What happens if my data fail these assumptions?

Firstly, don't panic! The first two of these assumptions are easily fixable, even if the last assumption is not. Lets go through the options as above:

  1. The one-way ANOVA is considered a robust test against the normality assumption. This means that it tolerates violations to its normality assumption rather well. As regards the normality of group data, the one-way ANOVA can tolerate data that is non-normal (skewed or kurtotic distributions) with only a small effect on the Type I error rate. However, platykurtosis can have a profound effect when your group sizes are small. This leaves you with two options: (1) transform your data using various algorithms so that the shape of your distributions become normally distributed or (2) choose the nonparametric Kruskal-Wallis H Test which does not require the assumption of normality.
  2. There are two tests that you can run that are applicable when the assumption of homogeneity of variances has been violated: (1) Welch or (2) Brown and Forsythe test. Alternatively, you could run a Kruskal-Wallis H Test. For most situations it has been shown that the Welch test is best. Both the Welch and Brown and Forsythe tests are available in SPSS Statistics (see our One-way ANOVA using SPSS Statistics guide).
  3. A lack of independence of cases has been stated as the most serious assumption to fail. Often, there is little you can do that offers a good solution to this problem.

How do I run a one-way ANOVA?

There are numerous ways to run a one-way ANOVA. However, we provide a comprehensive, step-by-step guide on how to do this using SPSS Statistics.

How do I report the results of a one-way ANOVA?

You will have calculated the following results or obtained them from SPSS Statistics:

Structure of results:

Source SS df MS F Sig.
Between SSb k-1 MSb MSb/MSw p value
Within SSw N-k MSw    
Total SSb + SSw N-1      

An example:

Source SS df MS F Sig.
Between 91.476 2 45.733 4.467 .021
Within 276.400 27 10.237    
Total 367.867 29      
Join the 10,000s of students, academics and professionals who rely on Laerd Statistics.TAKE THE TOUR

You will want to report this as follows:

There was a statistically significant difference between groups as determined by one-way ANOVA (F(2,27) = 4.467, p = .021). This is all you will need to write for the one-way ANOVA per se. However, in reality you will probably also want to report means ± standard deviations for your groups, as well as follow up a statistically significant result with a post hoc test. If you use SPSS Statistics, these descriptive statistics will be reported in the output along with the result from the one-way ANOVA. The general form of writing the result of a one-way ANOVA is as follows:

One-way ANOVA Result

where df = degrees of freedom.

You should not report the result as "significant difference", but instead report it as "statistically significant difference". This is because your decision as to whether the result is significant or not should not be based solely on your statistical test. Therefore, to indicate to readers that this "significance" is a statistical one, include this is your sentence.

Find out what else you have to do when you have a statistically significant ANOVA or a non-statistically significant ANOVA result on the next page.

« prev
1 234
next »