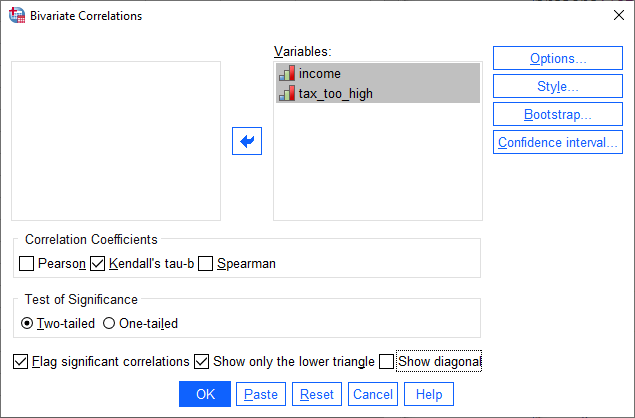
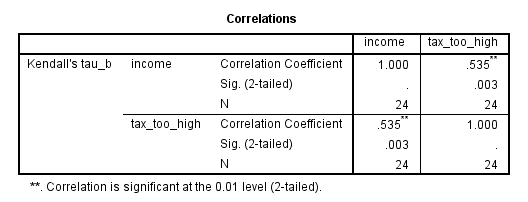
Kendall's Tau-b using SPSS Statistics

Introduction

Kendall's tau-b (τ_b) correlation coefficient (Kendall's tau-b, for short) is a nonparametric measure of the strength and direction of association that exists between two variables measured on at least an ordinal scale. It is considered a nonparametric alternative to the Pearson’s product-moment correlation when your data has failed one or more of the assumptions of this test. It is also considered an alternative to the nonparametric Spearman rank-order correlation coefficient (especially when you have a small sample size with many tied ranks). If you consider one of your variables as an independent variable and the other as a dependent variable, you might consider running a Somers' d test instead.

For example, you could use Kendall's tau-b to understand whether there is an association between exam grade and time spent revising (i.e., where there were six possible exam grades – A, B, C, D, E and F – and revision time was split into five categories: less than 5 hours, 5-9 hours, 10-14 hours, 15-19 hours, and 20 hours or more). Alternately, you could use Kendall's tau-b to understand whether there is an association between customer satisfaction and delivery time (i.e., where delivery time had four categories – next day, 2 working days, 3-5 working days, and more than 5 working days – and customer satisfaction was measured in terms of the level of agreement customers had with the following statement, "I am satisfied with the time it took for my parcel to be delivered", where the level of agreement had five categories: strongly agree, agree, neither agree nor disagree, disagree and strongly disagree).

This "quick start" guide shows you how to carry out Kendall's tau-b using SPSS Statistics. We show you the main procedure to carry out Kendall's tau-b in the Procedure section. However, first we introduce you to the assumptions that you must consider when carrying out Kendall's tau-b.

SPSS Statistics

Assumptions

When you choose to analyse your data using Kendall's tau-b, part of the process involves checking to make sure that the data you want to analyse can actually be analysed using Kendall's tau-b. You need to do this because it is only appropriate to use Kendall's tau-b if your data "passes" the assumptions that are required for Kendall's tau-b to give you a valid result. In practice, checking for these assumptions just adds a little bit more time to your analysis, requiring you to click of few more buttons in SPSS Statistics when performing your analysis, as well as think a little bit more about your data, but it is not a difficult task. These two assumptions are:

• Assumption #1: Your two variables should be measured on an ordinal or continuous scale. Examples of ordinal variables include Likert scales (e.g., a 7-point scale from strongly agree through to strongly disagree), amongst other ways of ranking categories (e.g., a 5-point scale explaining how much a customer liked a product, ranging from "Not very much" to "Yes, a lot"). Examples of continuous variables (i.e., interval or ratio variables) include revision time (measured in hours), intelligence (measured using IQ score), exam performance (measured from 0 to 100), weight (measured in kg), and so forth. You can learn more about ordinal and continuous variables in our article: Types of Variable.
• Assumption #2: Kendall's tau-b determines whether there is a monotonic relationship between your two variables. As such, it is desirable if your data would appear to follow a monotonic relationship, so that formally testing for such an association makes sense, but it is not a strict assumption or one that you are often able to assess.

In the section, Test Procedure in SPSS Statistics, we illustrate the SPSS Statistics procedure to perform Kendall's tau-b assuming that no assumptions have been violated. First, we set out the example we use to explain the Kendall's tau-b procedure in SPSS Statistics.