One-way ANOVA using Minitab
Introduction
The one-way analysis of variance (ANOVA) is used to determine whether the mean of a dependent variable is the same in two or more unrelated, independent groups of an independent variable. However, it is typically only used when you have three or more independent, unrelated groups, since an independent t-test is more commonly used when you have just two groups. If you have more than one dependent variable, you might need a one-way MANOVA.
For example, you can use a one-way ANOVA to determine whether weight loss is best achieved through exercise, diet, or exercise and diet combined (i.e., your dependent variable would be "weight loss", measured in kilograms, and your independent variable would be "intervention type", which has three groups: "exercise", "diet and "exercise and diet"). Alternately, a one-way ANOVA could be used to understand whether there is a difference in salary based on education level (i.e., your dependent variable would be "salary" and your independent variable would be "education level", which has three groups: "high school", "undergraduate degree" and "graduate degree").
When there is a statistically significant difference between the groups, it is possible to determine which specific groups were significantly different from each other using a post hoc test. You need to conduct a post hoc test because the one-way ANOVA is an omnibus test statistic and cannot tell you which specific groups were significantly different from each other; it only tells you that at least two groups were different.
This "quick start" guide shows you how to carry out a one-way ANOVA using Minitab, as well as how to interpret and report the results from this test. However, before we introduce you to this procedure, you need to understand the different assumptions that your data must meet in order for a one-way ANOVA to give you a valid result. We discuss these assumptions next.
Minitab
Assumptions
The one-way ANOVA has six assumptions. You cannot test the first three of these assumptions with Minitab because they relate to your study design and choice of variables. However, you should check whether your study meets these three assumptions before moving on. If these assumptions are not met, there is likely to be a different statistical test that you can use instead. Assumptions #1, #2 and #3 are explained below:
- Assumption #1: Your dependent variable should be measured on a continuous level (i.e., it is an interval or ratio variable). Examples of such dependent variables include height (measured in feet and inches), temperature (measured in °C), salary (measured in US dollars), revision time (measured in hours), intelligence (measured using IQ score), reaction time (measured in milliseconds), test performance (measured from 0 to 100), sales (measured in number of transactions per month), and so forth. If you are unsure whether your dependent variable is continuous (i.e., measured at the interval or ratio level), see our Types of Variable guide.
- Assumption #2: Your independent variable should consist of two or more categorical, independent (unrelated) groups. Examples of categorical variables include gender (e.g., two groups: male and female), ethnicity (e.g., three groups: Caucasian, African American and Hispanic), physical activity level (e.g., four groups: sedentary, low, moderate and high), and profession (e.g., five groups: surgeon, doctor, nurse, dentist, therapist).
- Assumption #3: You should have independence of observations, which means that there is no relationship between the observations in each group or between the groups themselves. For example, there must be different participants in each group with no participant being in more than one group. If you do not have independence of observations, it is likely you have "related groups", which means you will might need to use a one-way repeated measures ANOVA instead of the one-way ANOVA.
Assumptions #4, #5 and #6 relate to the nature of your data and can be checked using Minitab. You have to check that your data meets these assumptions because if it does not, the results you get when running a one-way ANOVA might not be valid. In fact, do not be surprised if your data violates one or more of these assumptions. This is not uncommon. However, there are possible solutions to correct such violations (e.g., transforming your data) such that you can still use a one-way ANOVA. Assumptions #4, #5 and #6 are explained below:
- Assumption #4: There should be no significant outliers. An outlier is simply a single case within your data set that does not follow the usual pattern (e.g., in a study of 100 students' IQ scores, where the mean score was 108 with only a small variation between students, one student had a score of 156, which is very unusual, and may even put her in the top 1% of IQ scores globally). The problem with outliers is that they can have a negative effect on the one-way ANOVA, reducing the accuracy of your results. Fortunately, when using Minitab to run a one-way ANOVA on your data, you can easily detect possible outliers.
- Assumption #5: Your dependent variable should be approximately normally distributed for each group of the independent variable. Your data need only be approximately normal for running a one-way ANOVA because it is quite "robust" to violations of normality, meaning that this assumption can be a little violated and still provide valid results. You can test for normality using the Shapiro-Wilk test for normality, which is easily tested for using Minitab.
- Assumption #6: There needs to be homogeneity of variances. You can test this assumption in Minitab using Levene's test for homogeneity of variances. Levene's test is very important when it comes to interpreting the results from a one-way ANOVA because Minitab is capable of producing different output depending on whether your data meets or fails this assumption.
In practice, checking for assumptions #4, #5 and #6 will probably take up most of your time when carrying out a one-way ANOVA. However, it is not a difficult task and Minitab provides all the tools you need to do this.
In the section, Test Procedure in Minitab, we illustrate the Minitab procedure required to perform a one-way ANOVA assuming that no assumptions have been violated. First, we set out the example we use to explain the one-way ANOVA procedure in Minitab.
Minitab
Example
An online retailer wants to get the best from its employees, as well as improve their working experience. Currently, employees in the retailer’s order fulfilment centre are not provided with any kind of entertainment whilst they work (e.g., no background music, television, etc.). However, the retailer wants to know whether providing music, which a few employees have requested, would lead to greater productivity, and if so, by how much.
Therefore, the researcher recruited a random sample of 60 employees. This sample of 60 participants was randomly split into three independent groups with 20 participants in each group: (a) a "control group" that did not listen to music; (b) a "treatment group" who listened to music, but had no choice of what they listened to; and (c) a second treatment group who listened to music and had a choice of what they listened to.
The experiment lasted for one month. At the end of the experiment, the "productivity" of the three groups was measured in terms of the "average number of packages processed per hour". Therefore, the dependent variable was "productivity" (measured in terms of the average number of packages processed per hour during the one month experiment), whilst the independent variable was "treatment type", where there were three independent groups: "No music" (control group), "Music - No choice" (treatment group A) and "Music - choice" (treatment group B).
A one-way ANOVA was used to determine whether there was a statistically significant difference in productivity between the three independent groups.
Note: The example and data used for this guide are fictitious. We have just created them for the purposes of this guide.
Minitab
Setup in Minitab
In Minitab, under column ![]() we entered the the values of the dependent variable, which we named Productivity, as follows:
we entered the the values of the dependent variable, which we named Productivity, as follows: ![]() . Then, under column
. Then, under column ![]() we entered the name of the independent variable , Music, as follows:
we entered the name of the independent variable , Music, as follows: ![]() . The three groups of the independent variable, Music, were: (a) "No music" for the control group; (b) "Music - No choice" for the treatment group who listened to music, but had no choice of what they listened to; and (c) "Music - Choice" for the treatment group who listened to music and had a choice of what they listened to, as shown below:
. The three groups of the independent variable, Music, were: (a) "No music" for the control group; (b) "Music - No choice" for the treatment group who listened to music, but had no choice of what they listened to; and (c) "Music - Choice" for the treatment group who listened to music and had a choice of what they listened to, as shown below:
Published with written permission from Minitab Inc.
Minitab
Test Procedure in Minitab
In this section, we show you how to analyse your data using a one-way ANOVA in Minitab when the six assumptions in the previous section, Assumptions, have not been violated. The procedure changed from Minitab 16 to Minitab 17. Therefore, we present the procedure for both below:
Minitab 16
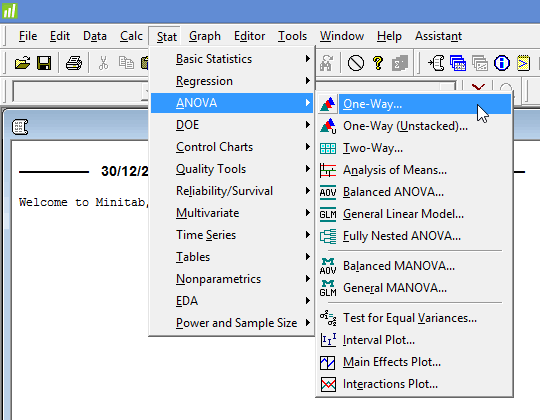
- Click Stat > ANOVA > One-Way... on the top menu, as shown below:

Published with written permission from Minitab Inc.
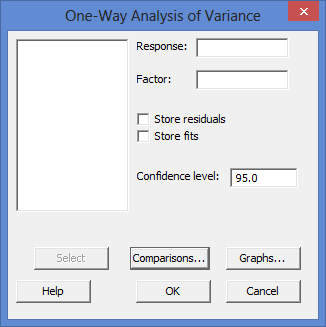
You will be presented with the following One-Way Analysis of Variance dialogue box:

Published with written permission from Minitab Inc.
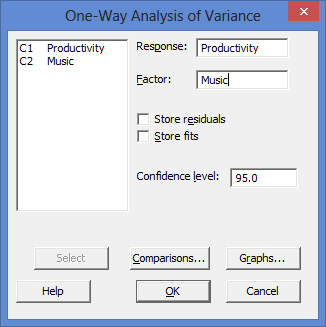
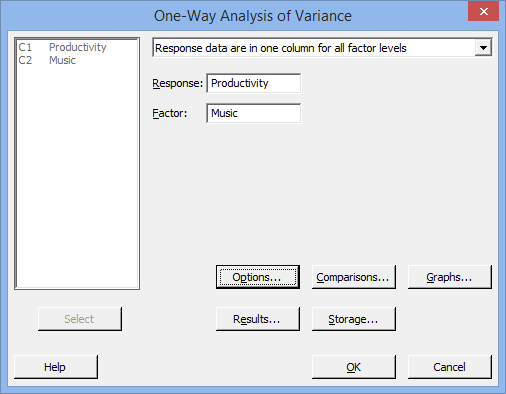
- Transfer the dependent variable, Productivity, into the Response: box and the independent variable, Music, into the Factor: box. To do this, you first need to click into the Response: box for the dependent variable to appear in the main left-hand box (e.g., C1 Productivity). This will activate the
 button (it is usually faded:
button (it is usually faded:  ). To transfer the variable into this box, select C1 Productivity in the main left-hand box and press the
). To transfer the variable into this box, select C1 Productivity in the main left-hand box and press the  button or simply double-click on C1 Productivity. You now need to do the same for C2 Music, but this time into the Factor: box. You will end up with the dialogue box shown below:
button or simply double-click on C1 Productivity. You now need to do the same for C2 Music, but this time into the Factor: box. You will end up with the dialogue box shown below:

Published with written permission from Minitab Inc.
Click on the
 button. The output that Minitab produces is shown below.
button. The output that Minitab produces is shown below.
Minitab 17
- Click Stat > ANOVA > One-Way... on the top menu, as shown below:

Published with written permission from Minitab Inc.
You will be presented with the following One-Way Analysis of Variance dialogue box:

Published with written permission from Minitab Inc.
- Transfer the dependent variable, Productivity, into the Response: box and the independent variable, Music, into the Factor: box. To do this, you first need to click into the Response: box for the dependent variable to appear in the main left-hand box (e.g., C1 Productivity). This will activate the
 button (it is usually faded:
button (it is usually faded:  ). To transfer the variable into this box, select C1 Productivity in the main left-hand box and press the
). To transfer the variable into this box, select C1 Productivity in the main left-hand box and press the  button or simply double-click on C1 Productivity. You now need to do the same for C2 Music, but this time into the Factor: box. You will end up with the dialogue box shown below:
button or simply double-click on C1 Productivity. You now need to do the same for C2 Music, but this time into the Factor: box. You will end up with the dialogue box shown below:

Published with written permission from Minitab Inc.
- Click on the
 button. The output that Minitab produces is shown below.
button. The output that Minitab produces is shown below.
Minitab
Output of the one-way ANOVA in Minitab
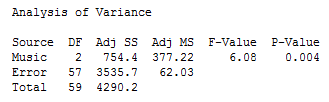
The Minitab output for a one-way ANOVA includes many useful statistics, including descriptive statistics for the groups that you compared. However, in this guide we focus on the Analysis of Variance table which reports the statistical significance of the one-way ANOVA, as shown below (for Minitab 17):
And for Minitab 16:

The statistical significance of the one-way ANOVA is found under the "P-Value" column ("P" column in Minitab 16). You can see that the significance level is 0.004 (i.e., p = .004). Since this is below 0.05 (i.e., p < .05), we can declare that the result is statistically significant. That is, there is a statistically significant difference in the mean productivity between the three different groups of the independent variable, Music (i.e., "No Music", "Music - No Choice" and "Music - Choice").
Note: We present the output from the one-way ANOVA above. However, since you should have tested your data for the assumptions we explained earlier in the Assumptions section, you will also need to interpret the Minitab output that was produced when you tested for them. This includes: (a) the boxplots you used to check if there were any significant outliers; (b) the output Minitab produces for your Shapiro-Wilk test for normality to determine normality; and (c) the output Minitab produces for Levene's test for homogeneity of variances. Also, remember that if your data failed any of these assumptions, the output that you get from the one-way ANOVA procedure (i.e., the output we discuss above) might no longer be valid and you will need to interpret the Minitab output that is produced when they fail (i.e., this includes different results).
Minitab
Reporting the output of the one-way ANOVA
When you report the output of your one-way ANOVA, it is good practice to include:
- A. An introduction to the analysis you carried out.
- B. Information about your sample, including how many participants were in each group of your independent groups (N) (N.B., this is particularly useful if the group sizes were unequal or there were missing values).
- C. A statement of whether there were statistically significant differences between your groups, including the observed F-value (F and F-Value for Minitab 16 and 17, respectively), degrees of freedom (DF), and significance level, or more specifically, the 2-tailed p-value (P and P-Value for Minitab 16 and 17, respectively).
Based on the Minitab output above, we could report the results of this study as follows:
- General
A one-way ANOVA was conducted to determine if productivity in a packing facility was different for groups with different physical activity levels. Participants were classified into three groups: No music (n = 20), Music - No choice (n = 20) and Music - Choice (n = 20). There was a statistically significant difference between groups as determined by a one-way ANOVA, F(2, 57) = 6.08, p = .004.
In addition to reporting the results as above, a diagram can be used to visually present your results. For example, you could do this using a bar chart with error bars (e.g., where the errors bars could be the standard deviation, standard error or 95% confidence intervals). This can make it easier for others to understand your results. Furthermore, you are increasingly expected to report "effect sizes" in addition to your one-way ANOVA results. Effect sizes are important because whilst the one-way ANOVA tells you whether differences between group means are "real" (i.e., different in the population), it does not tell you the "size" of the difference. Whilst Minitab will not produce these effect sizes for you using this procedure, there is a procedure in Minitab to do so.