Linear regression using Minitab

Introduction

Linear regression, also known as simple linear regression or bivariate linear regression, is used when we want to predict the value of a dependent variable based on the value of an independent variable. The dependent variable can also be referred to as the outcome, target or criterion variable, whilst the independent variable can also be referred to as the predictor, explanatory or regressor variable. We will refer to these as dependent and independent variables throughout this guide.

For example, you could use linear regression to understand whether test anxiety can be predicted based on revision time (i.e., the dependent variable would be "test anxiety", measured using an anxiety index, and the independent variable would be "revision time", measured in hours). Alternatively, you could use linear regression to understand whether cholesterol concentration (a fat in the blood linked to heart disease) can be predicted based on time spent exercising (i.e., the dependent variable would be "cholesterol concentration", measured in mmol/L, and the independent variable would be "time spent exercising", measured in hours).

Note: If you have two or more independent variables, rather than just one, you need to use multiple regression. Alternatively, if you just want to establish whether a linear relationship exists, but are not making predictions, you could use Pearson's correlation. If your dependent variable is dichotomous, you could use a binomial logistic regression.

In this guide, we show you how to carry out linear regression using Minitab, as well as interpret and report the results from this test. However, before we introduce you to this procedure, you need to understand the different assumptions that your data must meet in order for linear regression to give you a valid result. We discuss these assumptions next.

Minitab

Assumptions

Linear regression has seven assumptions. You cannot test the first two of these assumptions with Minitab because they relate to your study design and choice of variables. However, you should check whether your study meets these assumptions before moving on. If these assumptions are not met, there is likely to be a different statistical test that you can use instead. Assumptions #1 and #2 are explained below:

• Assumption #1: Your dependent variable should be measured at the continuous level (i.e., it is an interval or ratio variable). Examples of such continuous variables include height (measured in feet and inches), temperature (measured in °C), salary (measured in US dollars), revision time (measured in hours), intelligence (measured using IQ score), firm size (measured in terms of the number of employees), age (measured in years), reaction time (measured in milliseconds), grip strength (measured in kg), power output (measured in watts), test performance (measured from 0 to 100), sales (measured in number of transactions per month), academic achievement (measured in terms of GMAT score), and so forth. If you are unsure whether your dependent variable is continuous (i.e., measured at the interval or ratio level), see our Types of Variable guide.
• Assumption #2: Your independent variable should be measured at the continuous or categorical level. However, if you have a categorical independent variable, it is more common to use an independent t-test (for two groups) or one-way ANOVA (for three groups or more). In case you are unsure, examples of categorical variables include gender (e.g., two groups: male and female), ethnicity (e.g., three groups: Caucasian, African American and Hispanic), physical activity level (e.g., four groups: sedentary, low, moderate and high), and profession (e.g., five groups: surgeon, doctor, nurse, dentist, therapist). In this guide, we show you the linear regression procedure and Minitab output when both your dependent and independent variables were measured at the continuous level.

Assumptions #3, #4, #5, #6 and #7 relate to the nature of your data and can be checked using Minitab. You have to check that your data meets these assumptions because if it does not, the results you get when running a linear regression might not be valid. In fact, do not be surprised if your data violates one or more of these assumptions. This is not uncommon. However, there are possible solutions to correct such violations (e.g., transforming your data) such that you can still use a linear regression. Assumptions #3, #4, #5, #6 and #7 are explained below:

• Assumption #3: There needs to be a linear relationship between the dependent and independent variables. Whilst there are a number of ways to check whether a linear relationship exists between your two variables, we suggest creating a scatterplot using Minitab, where you can plot the dependent variable against your independent variable. You can then visually inspect the scatterplot to check for linearity. If the relationship displayed in your scatterplot is not linear, you will have to either run a non-linear regression analysis or "transform" your data, which you can do using Minitab.
• Assumption #4: There should be no significant outliers. An outlier is simply a case within your data set that does not follow the usual pattern. For example, consider a study examining the test anxiety of 500 students where anxiety was measured on a scale of 0-100, with 0 = no anxiety and 100 = maximum anxiety. The mean text anxiety score was 56 and the vast majority of students scored between 42 and 70. However, one student scores just 2 on the scale, with the second lowest test anxiety score being 36. As such, a student scoring just 2 on the scale "could" be considered an outlier. Where a score is an outlier this is problematic because outliers can have a negative effect on the regression equation that is used to predict the value of the dependent variable based on the independent variable. This will change the output that Minitab produces and reduce the predictive accuracy of your results. Fortunately, you can use Minitab to carry out casewise diagnostics to help you detect possible outliers.
• Assumption #5: You should have independence of observations, which you can easily check using the Durbin-Watson statistic, which is a simple test to run using Minitab.
• Assumption #6: Your data needs to show homoscedasticity, which is where the variances along the line of best fit remain similar as you move along the line. You can check whether your data showed homoscedasticity by plotting the regression standardized residuals against the regression standardized predicted value, which you can do using Minitab.
• Assumption #7: Finally, you need to check that the residuals (errors) of your two variables are approximately normally distributed. Two common methods to check this assumption include using either a histogram (with a superimposed normal curve) or a Normal P-P Plot. Again, you can do this using Minitab.

In practice, checking for assumptions #3, #4, #5, #6 and #7 will probably take up most of your time when carrying out linear regression. However, it is not a difficult task, and Minitab provides all the tools you need to do this.

In the section, Test Procedure in Minitab, we illustrate the Minitab procedure required to perform linear regression assuming that no assumptions have been violated. First, we set out the example we use to explain the linear regression procedure in Minitab.

Minitab

Example

An educator wants to determine whether students' exam scores were related to revision time. For example, as students spent more time revising, did their exam score also increase (a positive relationship); or did the opposite happen? The educator also wanted to know the proportion of exam score that revision time could explain, as well as being able to predict the exam score. The educator could then determine whether, for example, students that spent just 10 hours revising could still pass their exam. Therefore, the dependent variable was "exam score", measured on a scale from 0 to 100, and the independent variable was "revision time", measured in hours.

To carry out the analysis, the researcher recruited 40 students. The length of time revising (i.e., the independent variable, Revision time) and the exam scores (i.e., the dependent variable, Exam score) were recorded for all 40 participants. Expressed in variable terms, the researcher wanted to regress Exam score on Revision time. A linear regression was used to determine whether there was a statistically significant relationship between exam score and revision time.

Note: The example and data used for this guide are fictitious. We have just created them for the purposes of this guide.

Minitab

Setup in Minitab

In Minitab, we entered our two variables into the first two columns ( and ). Under column we entered the name of the dependent variable, Exam score, as follows: . Then, under column we entered the name of the independent variable, Revision time, as follows: . Finally, we entered the scores for the dependent variable, Exam score, into the column, and independent variable, Revision time, into the column. This is illustrated below:

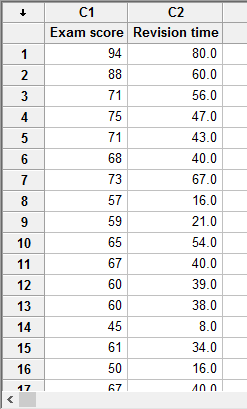
Published with written permission from Minitab Inc.

Note: It does not matter whether you enter the dependent variable or independent variable under C1 or C2. We have just entered the data into Minitab this way in our example.

Minitab

Test Procedure in Minitab

In this section, we show you how to analyze your data using a linear regression in Minitab when the seven assumptions set out in the Assumptions section have not been violated. Therefore, the three steps required to run a linear regression in Minitab are shown below:

1. Click Stat > Regression > Regression... on the top menu, as shown below:
   

   Published with written permission from Minitab Inc.

   
   You will be presented with the following Regression dialogue box:
   
   

   Published with written permission from Minitab Inc.

2. Transfer the dependent variable, C1   Exam score into the Response: box, and the independent variable, C2   Revision time into the Predictors: box. You will end up with the dialogue box shown below:
   

   Published with written permission from Minitab Inc.

   Note: To transfer the two variables, you first need to click inside the Response: box for your two variables to appear in the main left-hand box (e.g., C1   Exam score and C2   Revision time). This will activate the button (it is usually faded: ). Since the Response: box is where you put your dependent variable, you need to select the appropriate variable in the main left-hand box and either press the button or simply double-click on the variable (i.e., C1   Exam score in our example). You now need to follow the same procedure, but for the independent variable, which should be transferred into the Predictors: box (i.e., C2   Revision time in our example).

3. Click on the button. The output that Minitab produces is shown below.

Minitab

Output of the linear regression in Minitab

The Minitab output for a linear regression is shown below:

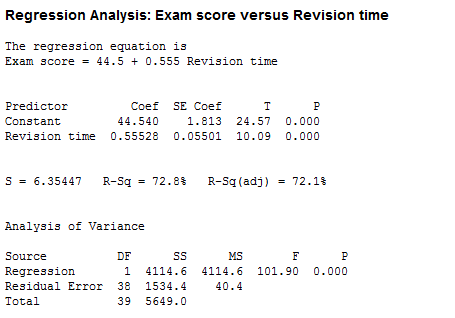
The output provides four important pieces of information:

• A. The R² value (the R-Sq value) represents the proportion of variance in the dependent variable that can be explained by our independent variable (technically it is the proportion of variation accounted for by the regression model above and beyond the mean model). However, R² is based on the sample and is a positively biased estimate of the proportion of the variance of the dependent variable accounted for by the regression model (i.e., it is too large).
• B. An adjusted R² value (the R-Sq(adj) value), which corrects positive bias to provide a value that would be expected in the population.
• C. The F value (the "F" column), degrees of freedom (the "DF" column) and statistical significance (2-tailed p-value) of the regression model (the "P" column).
• D. The coefficients for both variables (the "Coef" column), which is the information you need to predict the dependent variable, Exam score, using the independent variable, Revision time.

In this example, R² = 72.8%, whilst the adjusted R² = 72.1%, which means that the independent variable, Revision time, explains 72.8% of the variability of the dependent variable, Exam score. Adjusted R² is also an estimate of the effect size, which at 72.1%, is indicative of a large effect size according to Cohen's (1988) classification. In this example, the regression model is statistically significant, F(1, 38) = 101.90, p < .0005. This indicates that, overall, the model applied can statistically significantly predict the dependent variable, Exam score.

Note: In addition to the linear regression output above, you will also have to interpret (a) the scatterplots you used to check if there was a linear relationship between your two variables (i.e., Assumption #3); (b) casewise diagnostics to check there were no significant outliers (i.e., Assumption #4); (c) the output from the Durbin-Watson statistic to check for independence of observations (i.e., Assumption #5); (d) a scatterplot of the regression standardized residuals against the regression standardized predicted value to determine whether your data showed homoscedasticity (i.e., Assumption #6); and (e) a histogram (with superimposed normal curve) and Normal P-P Plot to check whether the residuals (errors) of the model were approximately normally distributed (i.e., Assumption #7) (see the Assumptions section earlier if you are unsure what these assumptions are). Remember that if your data failed any of these assumptions, the output that you get from the linear regression procedure (i.e., the output we discussed above) might not be valid, and you will have to take steps to deal with such violations (e.g., transforming your data using Minitab) or using a different statistical test.

Minitab

Reporting the output of the linear regression

When you report the output of your linear regression, it is good practice to include:

• A. An introduction to the analysis you carried out.
• B. Information about your sample, including any missing values.
• C. A statement of whether there was a statistically significant relationship between the dependent and independent variable, including the observed F-value (F), degrees of freedom (DF) and significance level, or more specifically, the 2-tailed p-value (P).
• D. A statement of the percentage/proportion of the variability in the dependent variable explained by the independent variable, which is the R² value (R-Sq).
• E. The regression equation for your model.

Based on the Minitab output above, we could report the results of this study as follows:

In addition to reporting the results as above, a diagram can be used to visually present your results. For example, you could use a scatterplot with confidence and prediction intervals (although it is not very common to add the last). This can make it easier for others to understand your results. Furthermore, you can use your linear regression equation to make predictions about the value of the dependent variable based on different values of the independent variable. Whilst Minitab does not produce these values as part of the linear regression procedure above, there is a procedure in Minitab that you can use to do so.

Portions of information contained in this publication/book are printed with permission of Minitab Inc. All such material remains the exclusive property and copyright of Minitab Inc. All rights reserved.