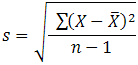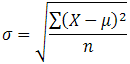Standard Deviation

Introduction

The standard deviation is a measure of the spread of scores within a set of data. Usually, we are interested in the standard deviation of a population. However, as we are often presented with data from a sample only, we can estimate the population standard deviation from a sample standard deviation. These two standard deviations - sample and population standard deviations - are calculated differently. In statistics, we are usually presented with having to calculate sample standard deviations, and so this is what this article will focus on, although the formula for a population standard deviation will also be shown.

When to use the sample or population standard deviation

We are normally interested in knowing the population standard deviation because our population contains all the values we are interested in. Therefore, you would normally calculate the population standard deviation if: (1) you have the entire population or (2) you have a sample of a larger population, but you are only interested in this sample and do not wish to generalize your findings to the population. However, in statistics, we are usually presented with a sample from which we wish to estimate (generalize to) a population, and the standard deviation is no exception to this. Therefore, if all you have is a sample, but you wish to make a statement about the population standard deviation from which the sample is drawn, you need to use the sample standard deviation. Confusion can often arise as to which standard deviation to use due to the name "sample" standard deviation incorrectly being interpreted as meaning the standard deviation of the sample itself and not the estimate of the population standard deviation based on the sample.

What type of data should you use when you calculate a standard deviation?

The standard deviation is used in conjunction with the mean to summarise continuous data, not categorical data. In addition, the standard deviation, like the mean, is normally only appropriate when the continuous data is not significantly skewed or has outliers.