Pearson's Correlation using Stata

Introduction

The Pearson product-moment correlation coefficient, often shortened to Pearson correlation or Pearson's correlation, is a measure of the strength and direction of association that exists between two continuous variables. The Pearson correlation generates a coefficient called the Pearson correlation coefficient, denoted as r. A Pearson's correlation attempts to draw a line of best fit through the data of two variables, and the Pearson correlation coefficient, r, indicates how far away all these data points are to this line of best fit (i.e., how well the data points fit this new model/line of best fit). Its value can range from -1 for a perfect negative linear relationship to +1 for a perfect positive linear relationship. A value of 0 (zero) indicates no relationship between two variables.

For example, you could use a Pearson's correlation to understand whether there is an association between exam performance and time spent revising (i.e., your two variables would be "exam performance", measured from 0-100 marks, and "revision time", measured in hours). If there was a moderate, positive association, we could say that more time spent revising was associated with better exam performance. Alternately, you could use a Pearson's correlation to understand whether there is an association between length of unemployment and happiness (i.e., your two variables would be "length of unemployment", measured in days, and "happiness", measured using a continuous scale). If there was a strong, negative association, we could say that the longer the length of unemployment, the greater the unhappiness.

In this guide, we show you how to carry out a Pearson's correlation using Stata, as well as interpret and report the results from this test. However, before we introduce you to this procedure, you need to understand the different assumptions that your data must meet in order for a Pearson's correlation to give you a valid result. We discuss these assumptions next.

Stata

Assumptions

There are four "assumptions" that underpin a Pearson's correlation. If any of these four assumptions are not met, analysing your data using a Pearson's correlation might not lead to a valid result. Since assumption #1 relates to your choice of variables, it cannot be tested for using Stata. However, you should decide whether your study meets this assumption before moving on.

• Assumption #1: Your two variables should be measured at the continuous level. Examples of such continuous variables include height (measured in feet and inches), temperature (measured in °C), salary (measured in US dollars), revision time (measured in hours), intelligence (measured using IQ score), reaction time (measured in milliseconds), test performance (measured from 0 to 100), sales (measured in number of transactions per month), and so forth. If you are unsure whether your two variables are continuous (i.e., measured at the interval or ratio level), see our Types of Variable guide.

  Note: If either of your two variables were measured on an ordinal scale, you need to use Spearman's correlation instead of Pearson's correlation. Examples of ordinal variables include Likert scales (e.g., a 7-point scale from "strongly agree" through to "strongly disagree"), amongst other ways of ranking categories (e.g., a 5-point scale for measuring job satisfaction, ranging from "most satisfied" to "least satisfied"; a 4-point scale determining how easy it was to navigate a new website, ranging from "very easy" to "very difficult; or a 3-point scale explaining how much a customer liked a product, ranging from "Not very much", to "It is OK", to "Yes, a lot").

Fortunately, you can check assumptions #2, #3 and #4 using Stata. When moving on to assumptions #2, #3 and #4, we suggest testing them in this order because it represents an order where, if a violation to the assumption is not correctable, you will no longer be able to use a Pearson's correlation. In fact, do not be surprised if your data fails one or more of these assumptions since this is fairly typical when working with real-world data rather than textbook examples, which often only show you how to carry out a Pearson's correlation when everything goes well. However, don't worry because even when your data fails certain assumptions, there is often a solution to overcome this (e.g., transforming your data or using another statistical test instead). Just remember that if you do not check that you data meets these assumptions or you do not test for them correctly, the results you get when running a Pearson's correlation might not be valid.

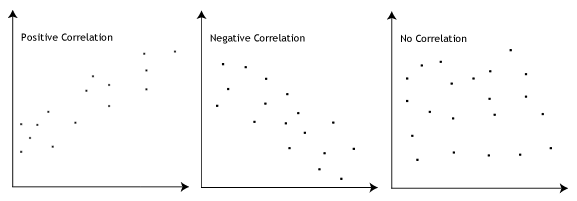
• Assumption #2: There needs to be a linear relationship between your two variables. Whilst there are a number of ways to check whether a Pearson's correlation exists, we suggest creating a scatterplot using Stata, where you can plot your two variables against each other. You can then visually inspect the scatterplot to check for linearity. Your scatterplot may look something like one of the following:
  
  
  
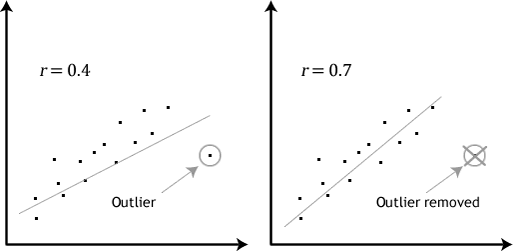
  If the relationship displayed in your scatterplot is not linear, you will have to either "transform" your data or perhaps run a Spearman's correlation instead, which you can do using Stata.
• Assumption #3: There should be no significant outliers. Outliers are simply single data points within your data that do not follow the usual pattern (e.g., in a study of 100 students' IQ scores, where the mean score was 108 with only a small variation between students, one student had a score of 156, which is very unusual, and may even put her in the top 1% of IQ scores globally). The following scatterplots highlight the potential impact of outliers:
  
  
  
  Pearson's r is sensitive to outliers, which can have a very large effect on the line of best fit and the Pearson correlation coefficient, leading to very difficult conclusions regarding your data. Therefore, it is best if there are no outliers or they are kept to a minimum. Fortunately, you can use Stata to detect possible outliers using scatterplots.
• Assumption #4: Your variables should be approximately normally distributed. In order to assess the statistical significance of the Pearson correlation, you need to have bivariate normality, but this assumption is difficult to assess, so a simpler method is more commonly used. This is known as the Shapiro-Wilk test of normality, which you can carry out using Stata.

In practice, checking for assumptions #2, #3 and #4 will probably take up most of your time when carrying out a Pearson's correlation. However, it is not a difficult task, and Stata provides all the tools you need to do this.

In the section, Test Procedure in Stata, we illustrate the Stata procedure required to perform a Pearson's correlation assuming that no assumptions have been violated. First, we set out the example we use to explain the Pearson's correlation procedure in Stata.

Stata

Example

Studies show that exercising can help prevent heart disease. Within reasonable limits, the more you exercise, the less risk you have of suffering from heart disease. One way in which exercise reduces your risk of suffering from heart disease is by reducing a fat in your blood, called cholesterol. The more you exercise, the lower your cholesterol concentration. Furthermore, it has recently been shown that the amount of time you spend watching TV – an indicator of a sedentary lifestyle – might be a good predictor of heart disease (i.e., that is, the more TV you watch, the greater your risk of heart disease).

Therefore, a researcher decided to determine if cholesterol concentration was related to time spent watching TV in otherwise healthy 45 to 65 year old men (an at-risk category of people). For example, as people spent more time watching TV, did their cholesterol concentration also increase (a positive relationship); or did the opposite happen?

To carry out the analysis, the researcher recruited 100 healthy male participants between the ages of 45 and 65 years old. The amount of time spent watching TV (i.e., the variable, time_tv) and cholesterol concentration (i.e., the variable, cholesterol) were recorded for all 100 participants. Expressed in variable terms, the researcher wanted to correlate cholesterol and time_tv.

Note: The example and data used for this guide are fictitious. We have just created them for the purposes of this guide.

Stata

Setup in Stata

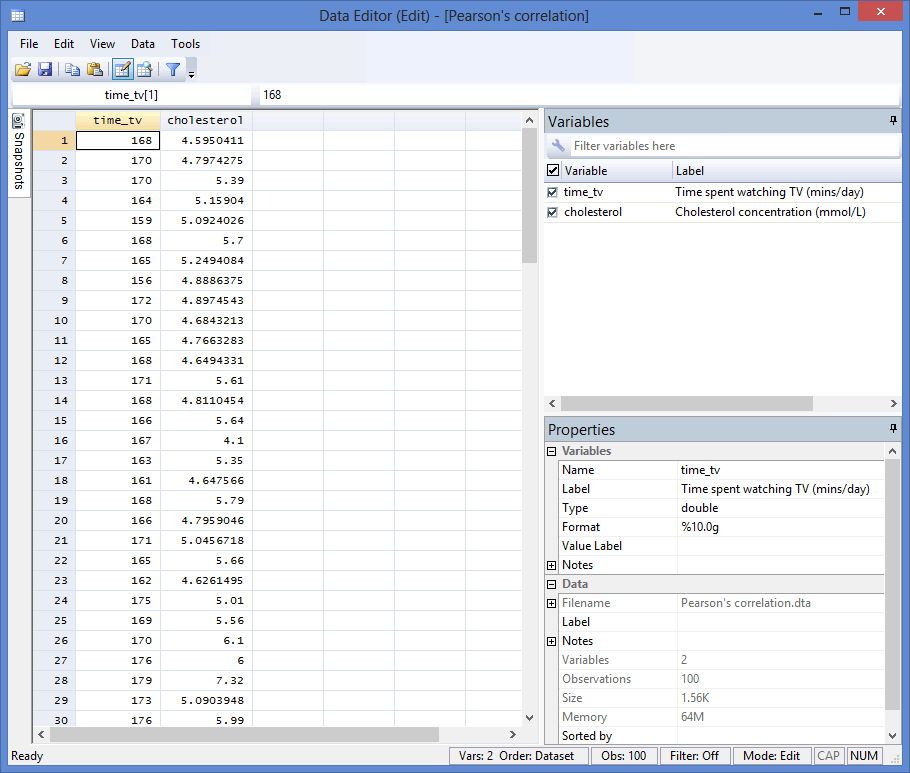
In Stata, we created two variables: (1) time_tv, which is the average daily time spent watching TV in minutes; and (2) cholesterol, which is the cholesterol concentration in mmol/L.

Note: It does not matter which variable you create first.

After creating these two variables – time_tv and cholesterol – we entered the scores for each into the two columns of the Data Editor (Edit) spreadsheet (i.e., the time in hours that the participants watched tv in the left-hand column (i.e., time_tv), and participants' cholesterol concentration in mmol/L in the right-hand column (i.e., cholesterol)), as shown below:

Published with written permission from StataCorp LP.

Stata

Test Procedure in Stata

In this section, we show you how to analyse your data using a Pearson's correlation in Stata when the four assumptions in the previous section, Assumptions, have not been violated. You can carry out a Pearson's correlation using code or Stata's graphical user interface (GUI). After you have carried out your analysis, we show you how to interpret your results. First, choose whether you want to use code or Stata's graphical user interface (GUI).

Code

The basic code to run a Pearson's correlation takes the form:

pwcorr VariableA VariableB

However, if you also want Stata to produce a p-value (i.e., the statistical significance level of your result), you need to add sig to the end of the code, as shown below:

pwcorr VariableA VariableB, sig

If you also want Stata to let you know whether your result is statistically significant at a particular level (e.g., where p < .05), you can set this p-value by adding it to the end of the code (e.g., (.05) where p < .05 or (.01) where p < .01), preceded by sig star (e.g., sig star(.05)), which places a star next to the correlation score if your result is statistically significant at this level. The code would take the form:

pwcorr VariableA VariableB, sig star(.05)

Finally, if you want Stata to display the number of observations (i.e., your sample size, N), you can do this by adding obs to the end of the code, as shown below:

pwcorr VariableA VariableB, sig star(.05) obs

Whatever code you choose to include should be entered into the box below:

Published with written permission from StataCorp LP.

Using our example where one variable is cholesterol and the other variable is time_tv, the required code would be one of the following:

pwcorr cholesterol time_tv

pwcorr cholesterol time_tv, sig

pwcorr cholesterol time_tv, sig star(.05)

pwcorr cholesterol time_tv, sig star(.05) obs

Since we wanted to include (a) the correlation coefficient, (b) the p-value at the .05 level and (c) the sample size (i.e., the number of observations), as well as (d) being notified whether our result was statistically significant at the .05 level, we entered the code, pwcorr cholesterol time_tv, sig star(.05) obs, and pressed the "Return/Enter" button on our keyboard, as shown below:

Published with written permission from StataCorp LP.

You can see the Stata output that will be produced here.

Graphical User Interface (GUI)

The three steps required to carry out a Pearson's correlation in Stata 12 and 13 are shown below:

1. Click Statistics > Summaries, tables, and tests > Summary and descriptive statistics > Pairwise correlations on the main menu, as shown below:
   

   Published with written permission from StataCorp LP.

   
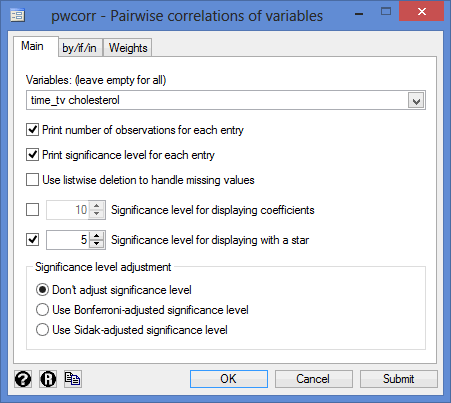
   You will be presented with the following pwcorr - Pairwise correlations of variables dialogue box:
   
   

   Published with written permission from StataCorp LP.

2. Select cholesterol and time_tv from within the Variables: (leave empty for all) box, using the button. Next, tick the Print number of observations for each entry, Print significance level for each entry and Significance level for displaying with a star boxes. You will end up with the following screen:
   

   Published with written permission from StataCorp LP.

   Note: It does not matter in which order you select your two variables from within the Variables: (leave empty for all) box.

3. Click on the button. This will generate the output.

Stata

Output of a Pearson's correlation in Stata

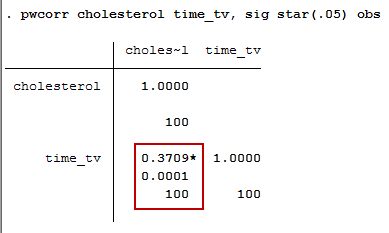
If your data passed assumption #2 (i.e., there was a linear relationship between your two variables), assumption #3 (i.e., there were no significant outliers) and assumption #4 (i.e., your two variables were approximately normally distributed), which we explained earlier in the Assumptions section, you will only need to interpret the following Pearson's correlation output in Stata:

Published with written permission from StataCorp LP.

The output contains three important pieces of information: (1) the Pearson correlation coefficient; (2) the level of statistical significance; and (3) the sample size. These three pieces of information are explained in more detail below:

• (1) The Pearson correlation coefficient, r, which shows the strength and direction of the association between your two variables, cholesterol and time_tv: This is shown in the first row of the red box. In our example, the Pearson correlation coefficient, r, is .3709. As the sign of the Pearson correlation coefficient is positive, you can conclude that there is a positive correlation between cholesterol concentration (cholesterol) and daily time spent watching TV (time_tv); that is, cholesterol concentration increases as time spent watching TV increases.

Note: Some would object to the description, "cholesterol concentration increases as time spent watching TV increases". The reason for this objection is rooted in the meaning of "increases". The use of this verb might suggest that the effect of this variable is causal and/or manipulatable such that you could increase the time spent watching TV (time_tv) in your participants and this would lead to an increase in their cholesterol concentration (cholesterol). This is not to say this might not be possible. However, this knowledge is not contained in the correlation, but in theory. As such, you might prefer to state the relationship as, "higher values of cholesterol concentration are associated/related to greater time spent watching TV".

The magnitude of the Pearson correlation coefficient determines the strength of the correlation. Although there are no hard-and-fast rules for assigning strength of association to particular values, some general guidelines are provided by Cohen (1988):

Coefficient Value	Strength of Association
0.1 < | r | < .3	small correlation
0.3 < | r | < .5	medium/moderate correlation
| r | > .5	large/strong correlation

where | r | means the absolute value or r (e.g., | r | > .5 means r > .5 and r < -.5). Therefore, the Pearson correlation coefficient in this example (r = .371) suggests a medium strength correlation. If instead, r = -.371, you would also have had a medium strength correlation, albeit a negative one.

The coefficient of determination is the proportion of variance in one variable that is "explained" by the other variable and is calculated as the square of the correlation coefficient (r²). In this example, you have a coefficient of determination, r², equal to 0.371² = 0.14. This can also be expressed as a percentage (i.e., 14%). Remember that this "explained" refers to being explained statistically, not causally.

• (2) The level of statistical significance (i.e., the p-value), and if the test is statistically significant, a star (*) next to the Pearson's correlation coefficient: This is shown in the second row of the red box. The results you have reported so far have only used the Pearson correlation coefficient to describe the relationship between the two variables in your sample. If you wish to test hypotheses about the linear relationship between your variables in the population your sample is from, you need to test the level of statistical significance. The level of statistical significance (p-value) of the correlation coefficient in this example is .0001, which means that there is a statistically significant relationship between the two variables: cholesterol concentration (cholesterol) and daily time spent watching TV (time_tv).
• (3) The sample size, n (i.e., the number of observations): This is shown in the third row of the red box, indicating that we have 100 participants in our study.

Note: We present the output from the Pearson's correlation above. However, since you should have tested your data for the assumptions we explained earlier in the Assumptions section, you will also need to interpret the Stata output that was produced when you tested for these assumptions. This includes: (a) the scatterplots you used to check if there was a linear relationship between your two variables (i.e., Assumption #2); (b) the same scatterplots that you will have used to check there were no significant outliers (i.e., Assumption #3); and (c) the Shapiro-Wilk test of normality to check whether your two variables were approximately normally distributed (i.e., Assumption #4). Also, remember that if your data failed any of these assumptions, the output that you get from the Pearson's correlation procedure (i.e., the output we discuss above) will no longer be relevant, and you may have to carry out a different statistical test to analyse your data.

Stata

Reporting the output of a Pearson's correlation

When you report the output of your Pearson's correlation, it is good practice to include:

• A. An introduction to the analysis you carried out.
• B. Information about your sample (including any missing values).
• C. The Pearson correlation coefficient, r, and degrees of freedom, which is the sample size minus 2 (e.g., for a sample size of 100, the degrees of freedom would be 98, as in our example).
• D. The statistical significance level (i.e., p-value) of your result.
• E. The coefficient of determination, r² (i.e., the proportion of variance in one variable that is "explained" by the other variable).

Based on the results above, we could report the results of this study as follows:

In addition to reporting the results as above, a diagram can be used to visually present your results. For example, you could do this using a scatterplot. This can make it easier for others to understand your results and is easily produced in Stata.