ANOVA with Repeated Measures using SPSS Statistics (cont...)
SPSS Statistics version 24
and earlier versions of SPSS Statistics
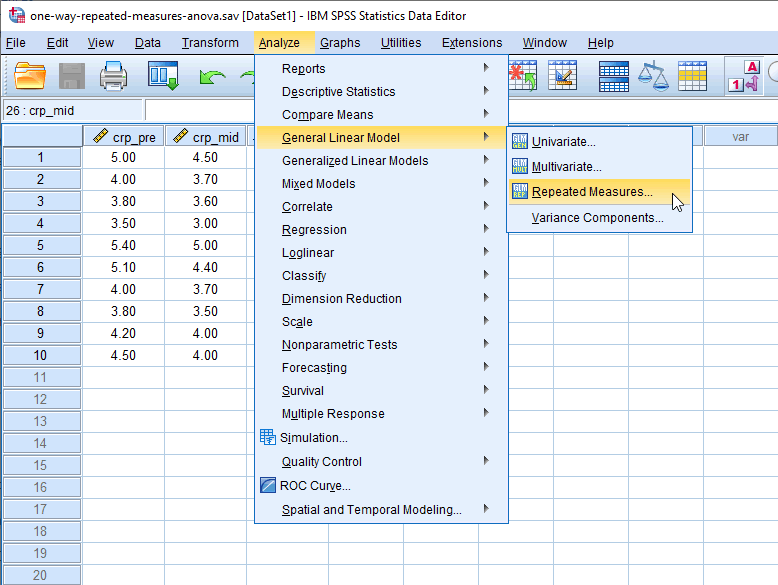
- Click Analyze > General Linear Model > Repeated measures... on the top menu, as shown below:

Published with written permission from SPSS Statistics, IBM Corporation.
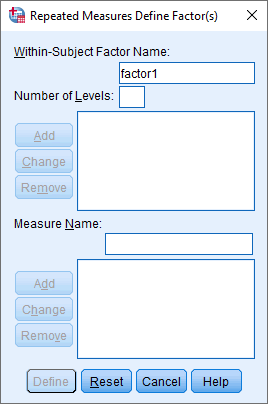
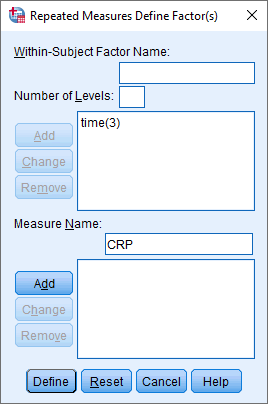
You will be presented with the Repeated Measures Define Factor(s) dialogue box, as shown below:

Published with written permission from SPSS Statistics, IBM Corporation.
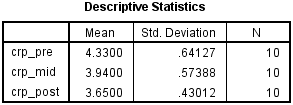
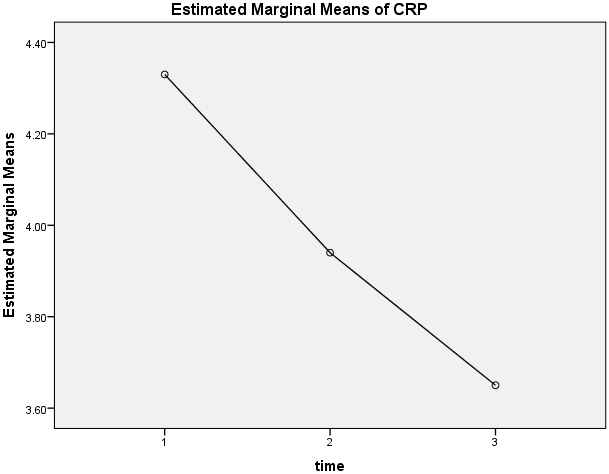
Explanation: This dialogue box is where you inform SPSS Statistics that the three variables – crp_pre, crp_mid and crp_post – are three levels of the within-subjects factor, time. Without doing this, SPSS Statistics will think that the three variables are just that, three separate variables.
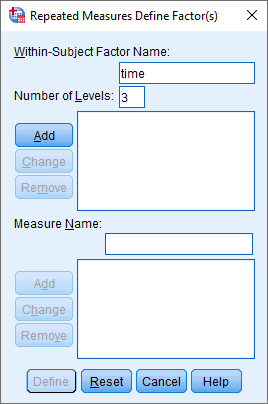
- In the Within-Subject Factor Name: box, replace "factor1" with a more meaningful name for your within-subjects factor. For example, we replaced "factor1" with "time" because this is the name of our within-subjects factor (i.e., time). Next, enter the number of levels of your within-subjects factor into the Number of Levels: box. For example, our within-subjects factor, time, has three levels, representing the three time points when our dependent variable, CRP, was measured (i.e., pre-intervention, crp_pre, mid-intervention, crp_mid, and post-intervention, crp_post). Therefore, we entered "3" into the Number of Levels: box, as shown below:

Published with written permission from SPSS Statistics, IBM Corporation.
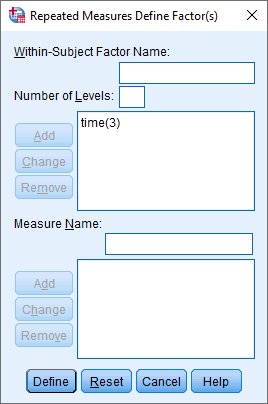
Click on the button and you will be presented with the following screen:
button and you will be presented with the following screen:

Published with written permission from SPSS Statistics, IBM Corporation.
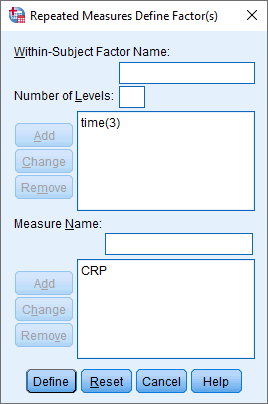
- In the Measure Name: box, enter a name that reflects the name of your dependent variable. Since our dependent variable is CRP, we entered "CRP", as shown below:

Published with written permission from SPSS Statistics, IBM Corporation.
Click on the button and you will get the following screen:
button and you will get the following screen:

Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
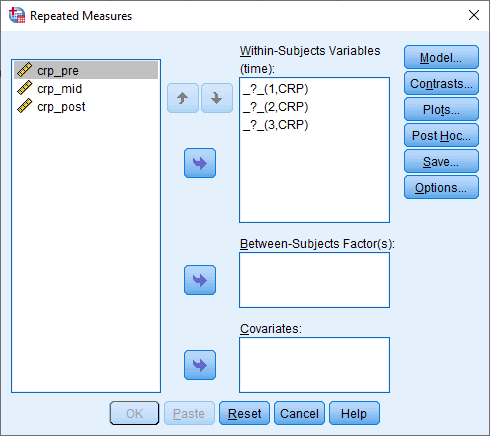
 button and you will be presented with the Repeated Measures dialogue box, as shown below:
button and you will be presented with the Repeated Measures dialogue box, as shown below:

Published with written permission from SPSS Statistics, IBM Corporation.
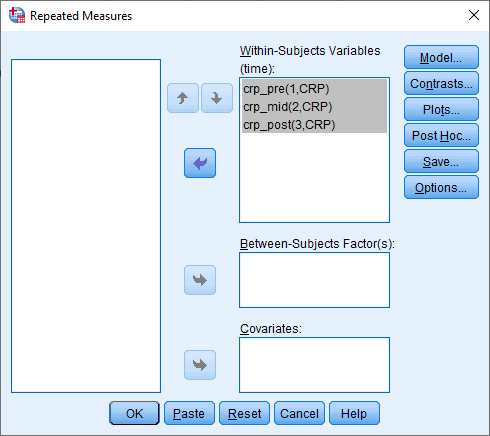
- Transfer crp_pre, crp_mid and crp_post into the "_?_(1,CRP)", "_?_(2,CRP)" and "_?_(3,CRP)" placeholders respectively in the Within-Subjects Variables (time): box, by highlighting all the variables in the left-hand box (by clicking on them whilst holding down the shift-key), and then clicking on the top
 button. You will end up with the following screen:
button. You will end up with the following screen:

Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
 button. You will be presented with the Repeated Measures: Profile Plots dialogue box, as shown below:
button. You will be presented with the Repeated Measures: Profile Plots dialogue box, as shown below:

Published with written permission from SPSS Statistics, IBM Corporation.
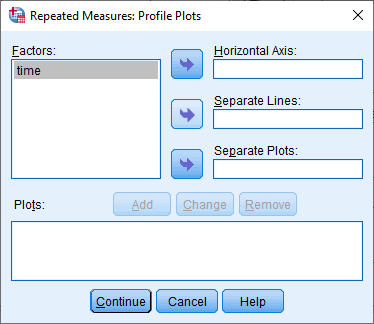
- Transfer the within-subjects factor, time, from the Factors: box into the Horizontal Axis: box by clicking on the top
 button. You will end up with the following screen:
button. You will end up with the following screen:

Published with written permission from SPSS Statistics, IBM Corporation.
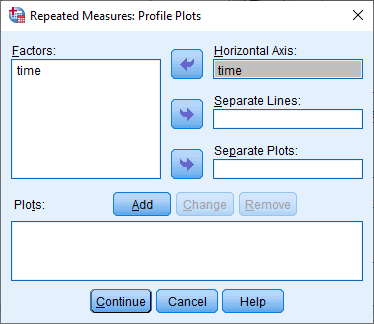
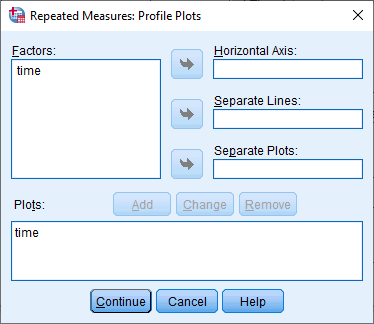
- Click on the
 button. This will transfer "time" from to the Plots: box, as shown below:
button. This will transfer "time" from to the Plots: box, as shown below:

Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
 button and you will be returned to the Repeated Measures dialogue box.
button and you will be returned to the Repeated Measures dialogue box.
- Click on the
 button and you will be presented with the Repeated Measures: Options dialogue box, as shown below:
button and you will be presented with the Repeated Measures: Options dialogue box, as shown below:

Published with written permission from SPSS Statistics, IBM Corporation.
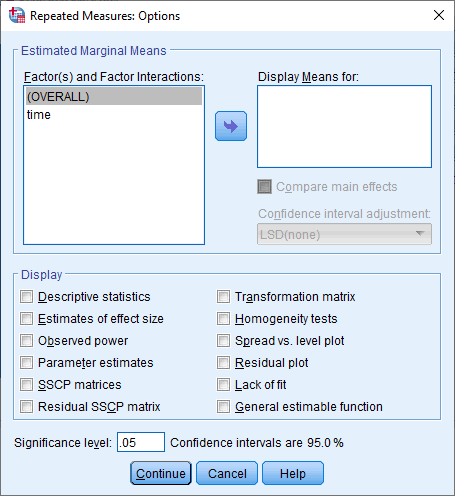
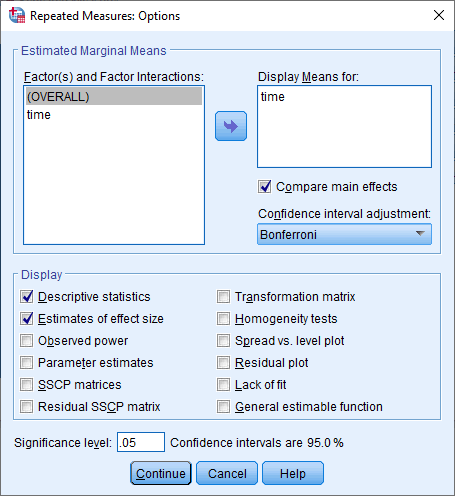
- Transfer time from the Factor(s) and Factor Interactions: box to the Display Means for: box using the
 button. This will activate the Compare main effects checkbox (i.e., it will no longer be greyed out). Tick this checkbox and select
button. This will activate the Compare main effects checkbox (i.e., it will no longer be greyed out). Tick this checkbox and select  from the drop-down menu under Confidence interval adjustment:. Next, in the –Display– area, tick the Descriptive statistics and Estimates of effect size checkboxes. You will be presented with the following screen:
from the drop-down menu under Confidence interval adjustment:. Next, in the –Display– area, tick the Descriptive statistics and Estimates of effect size checkboxes. You will be presented with the following screen:

Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
 button and you will be returned to the Repeated Measures dialogue box.
button and you will be returned to the Repeated Measures dialogue box.
- Click on the
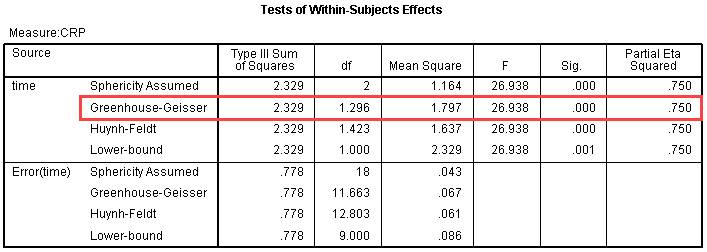
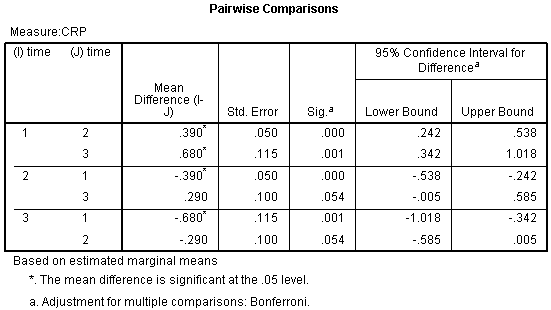
 button. This will generate the output.
button. This will generate the output.