Wilcoxon signed-rank test using Minitab

Introduction

The Wilcoxon signed-rank test determines whether there is a statistically significant difference in the median of a dependent variable between two related groups. It is the nonparametric equivalent to the paired t-test. As the Wilcoxon signed-ranks test does not assume normality of the differences of the two related groups, it can be used when this assumption has been violated and the use of the paired t-test is inappropriate.

For example, you could use a Wilcoxon signed-rank test to determine whether there is a difference in the number of customer complaints before and after a training course for sales reps designed to improve their customer interactions (i.e., the dependent variable would be “customer complaints”, and the two related groups would be the two different “time points”; that is, the number of customer complaints “before” the training course and the number of customer complaints “after“ the training course. Alternately, you could use a Wilcoxon signed-rank test to understand whether there is a difference in productivity based on whether packers in a factory listen to background music (i.e., the dependent variable would be "productivity", measured in terms of the number of parcels packers processed per day, and the two related groups would be the two different "conditions" participants were exposed to; that is, the number of parcels processed when packers listen to background music (condition A) compared to the number of parcels processed when packers do not listen to background music (condition B)).

In this guide, we show you how to carry out a Wilcoxon signed-rank test using Minitab, as well as interpret and report the results from this test. However, before we introduce you to this procedure, you need to understand the different assumptions that your data must meet in order for a Wilcoxon signed-rank test to give you a valid result. We discuss these assumptions next.

Minitab

Assumptions

The Wilcoxon signed-rank test has three "assumptions". You cannot test the first two of these assumptions with Minitab because they relate to your study design and choice of variables. However, you should check whether your study meets these two assumptions before moving on. If these assumptions are not met, there is likely to be a different statistical test that you can use instead. Assumptions #1 and #2 are explained below:

• Assumption #1: Your dependent variable should be measured at a continuous level (i.e., they are interval or ratio variables) or ordinal level. Examples of such continuous variables include height (measured in feet and inches), temperature (measured in ^oC), salary (measured in US dollars), revision time (measured in hours), intelligence (measured using IQ score), firm size (measured in terms of the number of employees), age (measured in years), reaction time (measured in milliseconds), grip strength (measured in kg), power output (measured in watts), test performance (measured from 0 to 100), sales (measured in number of transactions per month), academic achievement (measured in terms of GMAT score), and so forth. Examples of ordinal variables include Likert items (e.g., a 7-point scale from "strongly agree" through to "strongly disagree"), amongst other ways of ranking categories (e.g., a 5-point scale explaining how much a customer liked a product, ranging from "Not very much" to "Yes, a lot"). If you are unsure whether your dependent variable is continuous (i.e., measured at the interval or ratio level) or ordinal, see our Types of Variable guide.
• Assumption #2: Your independent variable should consist of two categorical, "related groups" or "matched pairs". "Related groups" indicates that the same participants are present in both groups. The reason that it is possible to have the same participants in each group is because each participant has been measured on two occasions on the same dependent variable. For example, you might have measured 100 participants' salary in US dollars (i.e., the dependent variable) before and after they took an MBA to improve their salary (i.e., the two "time points" where participants' salary was measured – "before" and "after" the MBA course – reflect the two "related groups" of the independent variable). Since the same participants were measured at these two time points, the groups are related. It is also common for related groups to reflect two different conditions that all participants undergo (i.e., these conditions are sometimes called interventions, treatments or trials). For example, you might have measured 50 participants' test anxiety (i.e., the dependent variable) when they underwent a hypnotherapy programme (condition A) compared to undergoing a counselling session (condition B) designed to reduce such anxiety (i.e., the two "conditions" where participants' test anxiety was measured – "condition A" and "condition B" – reflect the two "related groups" of the independent variable).

Assumption #3 relates to the nature of your data and can be checked using Minitab. You have to check that your data meets this assumption because if it does not, the results you get when running a Wilcoxon signed-rank test might not be valid. In fact, do not be surprised if your data violates this assumption. This is not uncommon. However, there are possible solutions to correct such violations (e.g., transforming your data) such that you can still use a Wilcoxon signed-rank test. Assumption #3 is explained below:

• Assumption #3: The distribution of the differences between the two related groups are symmetrical in shape (i.e., the distribution of differences between the scores of both groups of the independent variable – for example, the difference scores of "carbohydrate-only drink" and "carbohydrate-protein drink" trials – are symmetrical in shape). If the distribution of differences is symmetrically shaped, you can analyse your study using the Wilcoxon signed-rank test. If not, it may be possible to transform your data to achieve a symmetrically-shaped distribution of differences. However, if this option is not possible or desirable (Altman, 1999), you might run a sign test instead of the Wilcoxon signed-rank test since the sign test does not require this assumption to be met.

In practice, checking for assumption #3 will probably take up most of your time when carrying out a Wilcoxon signed-rank test. However, it is not a difficult task, and Minitab provides all the tools you need to do this.

In the section, Test Procedure in Minitab, we illustrate the Minitab procedure required to perform a Wilcoxon signed-rank test assuming that no assumptions have been violated. First, we set out the example we use to explain the Wilcoxon signed-rank test procedure in Minitab.

Minitab

Example

A company researcher wants to test a new formula for a sports drink that has been designed to improve running performance. Instead of the regular "carbohydrate-only" drink that the company produces, this new sports drink contains a "carbohydrate-protein" formula. The researcher would like to know whether this new carbohydrate-protein sports drink leads to a difference in running performance compared to the carbohydrate-only sports drink. Therefore, the dependent variable was "running performance", and the independent variable was "formula", which consisted of two related groups: "carbohydrate-protein" and "carbohydrate-only".

To carry out the experiment, the researcher recruited 20 middle-distance runners. All of these participants performed two trials in which they had to run as far as possible for 2 hours on a treadmill. In one of the trials, all 20 participants drank from a bottle containing the carbohydrate-only formula. In the other trial, the same 20 participants drank from a bottle containing the carbohydrate-protein formula. Whilst all participants completed both trials, the order in which they underwent the trials differed, which is known as counterbalancing (i.e., 10 of the 20 participants completed the trial with the carbohydrate-only drink first, and then the trial with the carbohydrate-protein drink second, whilst the other 10 participants started with the carbohydrate-protein trial and then undertook the carbohydrate-only trial). At the end of the two trials, the distance each participant ran (in km) was recorded.

A Wilcoxon signed-rank test was used to determine whether there was a statistically significant difference in distance run between the two trials (i.e., when using the carbohydrate-protein drink compared to the carbohydrate-only drink).

Minitab

Setup in Minitab

In Minitab, we set up the two related groups as though they were two variables: (a) the first related group, carb, was entered under column , as follows: ; and (b) the second related group, carb_protein, was entered under column , as follows: . Then, we entered the scores on the dependent variable for each of the two related groups (i.e., the distance run for each participant after taking the carbohydrate-only drink in the carb column and the distance run for the same participants after taking the carbohydrate-protein drink in the carb_protein column). Finally, we calculated the difference scores between carb and carb_protein, which were automatically entered under column into the variable, difference, as follows: . This is illustrated below:

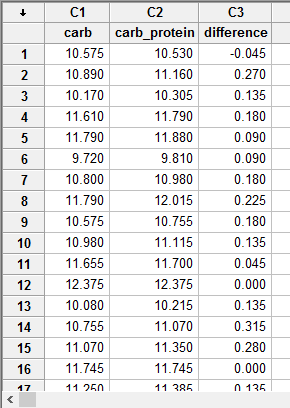
Published with written permission from Minitab Inc.

Note: The difference scores that you need when running a Wilcoxon signed-rank test in Minitab are not automatically calculated. Therefore, you need to run the Calc > Calculator... procedure.

Minitab

Test Procedure in Minitab

In this section, we show you how to analyse your data using a Wilcoxon signed-rank test in Minitab when the three assumptions in the previous section, Assumptions, have not been violated. Therefore, the three steps required to run a Wilcoxon signed-rank test in Minitab are shown below:

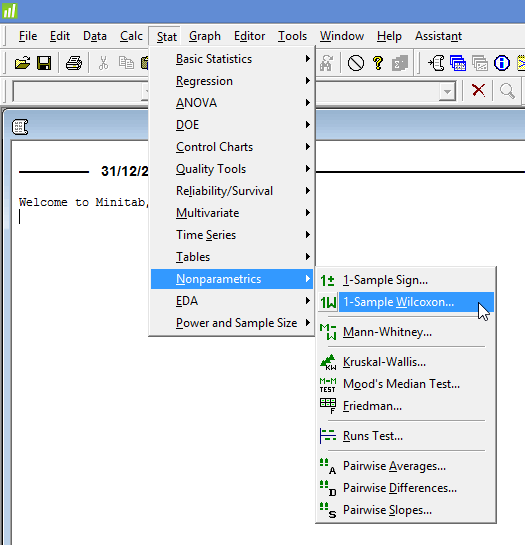
1. Click Stat > Nonparametrics > 1-Sample Wilcoxon... on the top menu, as shown below:
   

   Published with written permission from Minitab Inc.

   
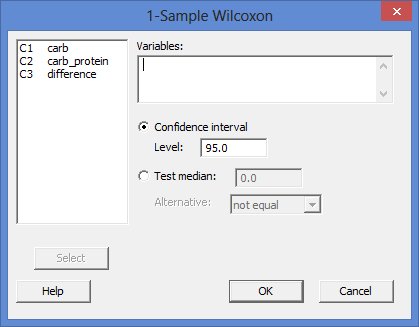
   You will be presented with the following 1-Sample Wilcoxon dialogue box:
   
   

   Published with written permission from Minitab Inc.

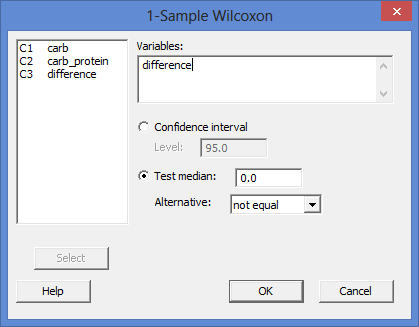
2. Enter the difference score, difference, into the Variables: box, and then select the Test median: option. Leave the value at 0.0 in the Test median: box and keep the alternative hypothesis set at not equal in the Alternative: box. You will end up with the dialogue box shown below:
   

   Published with written permission from Minitab Inc.

   Note 1: To transfer the difference score, difference, you first need to click inside the Variables: box for your two related groups to appear in the main left-hand box (e.g., C1   carb and C2   carb_protein), as well as the difference score (e.g., C3   difference). This will activate the button (it is usually faded: ). 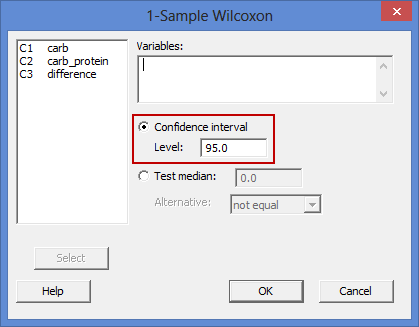To transfer the difference score, difference, into the Variables: box, you can now either select C3   difference in the main left-hand box and press the button or simply double-click on C3   difference.

   Note 2: By default, Minitab uses 95% confidence intervals, which equates to declaring statistical significance at the p < .05 level. If you want to change the value of the confidence interval, select the Confidence interval option and enter the new value into the Level: box (e.g., a value of 99.0 would equate to declaring statistical significance at the p < .01 level), highlighted in red below:
   
   

3. Click on the button. The output that Minitab produces is shown below.

Minitab

Output of the Wilcoxon signed-rank test in Minitab

The Minitab output for the Wilcoxon signed-rank test is shown below:

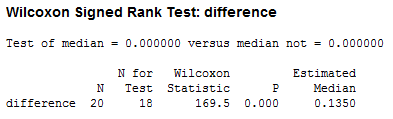
This output provides information about the difference (i.e., the difference between carb_protein and carb), including the sample size (the "N" column), the size for the test (the "N for Test" column), Wilcoxon signed-rank test statistic, W (the "Wilcoxon Statistic" column), the statistical significance (2-tailed p-value) of the Wilcoxon signed-rank test (the "P" column) and estimated median (the "Estimated Median" column). As the p-value is less than 0.05 (i.e., p < .05), it can be concluded that there is a statistically significant difference between our two related groups (carb and carb_protein). In other words, the difference in running performance between the carbohydrate-only and carbohydrate-protein drinks is not equal to zero.

Note: We present the output from the Wilcoxon signed-rank test above. However, since you should have tested your data for the assumptions we explained earlier in the Assumptions section, you will also need to interpret the Minitab output that was produced when you tested for them. This includes the histogram you need to determine whether the distribution of the differences between your two related groups are symmetrical in shape. Also, remember that if your data failed this assumption, the output that you get from the Wilcoxon signed-rank test procedure (i.e., the output we discuss above) might no longer be valid and you will have to take steps to deal with such violations (e.g., transforming your data using Minitab) or use a different statistical test instead.

Minitab

Reporting the output of the Wilcoxon signed-rank test

When you report the output of your Wilcoxon signed-rank test, it is good practice to include:

• A. An introduction to the analysis you carried out.
• B. Information about your sample, including how many participants were in each group of your two related groups (N.B., this is particularly useful if the group sizes were unequal or there were missing values).
• C. A statement of whether there were statistically significant differences between your two related groups, including the relevant median difference (Estimated Median), Wilcoxon signed-rank test statistic, W (Wilcoxon Statistic), and significance level, or more specifically, the 2-tailed p-value (P).

Based on the Minitab output above, we could report the results of this study as follows:

Portions of information contained in this publication/book are printed with permission of Minitab Inc. All such material remains the exclusive property and copyright of Minitab Inc. All rights reserved.