Paired t-test using Minitab

Introduction

The paired t-test (also known as the paired-samples t-test or dependent t-test) determines whether there is a statistically significant difference in the mean of a dependent variable between two related groups.

For example, you could use a paired t-test to determine whether there is a difference in students' test anxiety before and after undergoing a hypnotherapy programme designed to reduce stress (i.e., the dependent variable would be "test anxiety", and the two related groups would be the two different "time points"; that is, test anxiety "before" and "after" undergoing the hypnotherapy programme). Alternately, you could use a paired t-test to understand whether there is a difference in athletes' 100m sprint times when using a protein supplement compared to not using a supplement (i.e., the dependent variable would be "100m sprint time", and the two related groups would be the two different "conditions" participants were exposed to; that is, 100m sprint times when taking the protein supplement (condition A) compared 100m sprint times when not taking a supplement (condition B)).

In this guide, we show you how to carry out a paired t-test using Minitab, as well as interpret and report the results from this test. However, before we introduce you to this procedure, you need to understand the different assumptions that your data must meet in order for a paired t-test to give you a valid result. We discuss these assumptions next.

Minitab

Assumptions

The paired t-test has four "assumptions". You cannot test the first two of these assumptions with Minitab because they relate to your study design and choice of variables. However, you should check whether your study meets these two assumptions before moving on. If these assumptions are not met, there is likely to be a different statistical test that you can use instead. Assumptions #1 and #2 are explained below:

• Assumption #1: Your dependent variable should be measured at the continuous level (i.e., they are interval or ratio variables). Examples of such continuous variables include height (measured in feet and inches), temperature (measured in ^oC), salary (measured in US dollars), revision time (measured in hours), intelligence (measured using IQ score), firm size (measured in terms of the number of employees), age (measured in years), reaction time (measured in milliseconds), grip strength (measured in kg), power output (measured in watts), test performance (measured from 0 to 100), sales (measured in number of transactions per month), academic achievement (measured in terms of GMAT score), and so forth. If you are unsure whether your dependent variable is continuous (i.e., measured at the interval or ratio level), see our Types of Variable guide.
• Assumption #2: Your independent variable should consist of two categorical, "related groups" or "matched pairs". "Related groups" indicates that the same participants are present in both groups. The reason that it is possible to have the same participants in each group is because each subject has been measured on two occasions on the same dependent variable. For example, you might have measured 100 participants' salary in US dollars (i.e., the dependent variable) before and after they took an MBA to improve their salary (i.e., the two "time points" where participants' salary was measured – "before" and "after" the MBA course – reflect the two "related groups" of the independent variable). Since the same participants were measured at these two time points, the groups are related. It is also common for related groups to reflect two different conditions that all participants undergo (i.e., these conditions are sometimes called interventions, treatments or trials). For example, you might have measured 50 participants' test anxiety (i.e., the dependent variable) when they underwent a hypnotherapy programme (condition A) compared to undergoing a counselling session (condition B) designed to reduce such anxiety (i.e., the two "conditions" where participants' test anxiety was measured – "condition A" and "condition B" – reflect the two "related groups" of the independent variable).

Assumptions #3 and #4 relate to the nature of your data and can be checked using Minitab. You have to check that your data meets these assumptions because if it does not, the results you get when running a paired t-test might not be valid. In fact, do not be surprised if your data violates one or both of these assumptions. This is not uncommon. However, there are possible solutions to correct such violations (e.g., transforming your data) such that you can still use a paired t-test. Assumptions #3 and #4 are explained below:

• Assumption #3: There should be no significant outliers in the differences between the two related groups. An outlier is simply a case within your data set that does not follow the usual pattern. For example, consider a study examining the test anxiety of 500 students where anxiety was measured on a scale of 0-100, with 0 = no anxiety and 100 = maximum anxiety. The mean text anxiety score was 56 and the vast majority of students scored between 42 and 70. However, one student scores just 2 on the scale, with the second lowest test anxiety score being 36. As such, a student scoring just 2 on the scale "could" be considered an outlier. Where a score is an outlier this is problematic because outliers can have a disproportionately negative effect on the paired t-test, distorting the differences between the two related groups (whether increasing or decreasing the scores on the dependent variable), which reduces the accuracy of your results. In addition, they can affect the statistical significance of the test. Fortunately, when using Minitab to run a paired t-test on your data, you can easily detect possible outliers.
• Assumption #4: The distribution of the differences of the dependent variable between the two related groups should be approximately normally distributed. We talk about the paired t-test only requiring approximately normal data because it is quite "robust" to violations of normality, meaning that the assumption can be a little violated and still provide valid results. You can test for normality using the Shapiro-Wilk test of normality, which is easily tested for using Minitab. If you do not have normally distributed difference scores, you might consider running a Wilcoxon signed-rank test instead.

In practice, checking for assumptions #3 and #4 will probably take up most of your time when carrying out a paired t-test. However, it is not a difficult task, and Minitab provides all the tools you need to do this.

In the section, Test Procedure in Minitab, we illustrate the Minitab procedure required to perform a paired t-test assuming that no assumptions have been violated. First, we set out the example we use to explain the paired t-test procedure in Minitab.

Minitab

Example

A researcher wants to determine whether a hypnotherapy programme can help to reduce cigarette consumption amongst long-term smokers, defined as people that have been regular smokers for more than 10 years. Therefore, the dependent variable was "cigarette consumption", measured in terms of the average number of cigarettes smoked, and the independent variable was "time", which consisted of two related groups: "before" and "after" the hypnotherapy programme.

To carry out the experiment, the researcher recruited 20 long-term smokers. All of these 20 participants took part in the intervention, which was a 6 week hypnotherapy programme designed to help them quit smoking. The cigarette consumption of the participants was first recorded "before" the intervention (i.e., pre-intervention) and then for a second time "after" the intervention (i.e., post-intervention). This is typically known as a "pre-test post-test" study design.

A paired t-test was used to determine whether there was a statistically significant difference in cigarette consumption before and after the hypnotherapy programme.

Minitab

Setup in Minitab

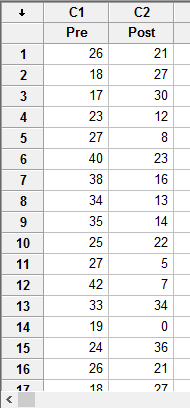
In Minitab, we set up the two related groups as though they were two variables. Therefore, under column we entered the name of the first related group, Pre, as follows: . Then, under column we entered the name of the second related group, Post, as follows: . Finally, we entered the scores on the dependent variable for each of the two related groups (i.e., the cigarette consumption for each participant before the hypnotherapy programme in the Pre column and the cigarette consumption for the same participants after the hypnotherapy programme in the Post column). This is illustrated below:

Published with written permission from Minitab Inc.

Note: If you do have all the data for your two related groups, as in our example above, but only the summarized data of the differences between your two related groups (i.e., the sample size, mean difference and standard deviation of the difference), Minitab can still run a paired t-test on your data. However, you will need to set up your data differently in order to do this.

Minitab

Test Procedure in Minitab

In this section, we show you how to analyse your data using a paired t-test in Minitab when the four assumptions set out in the Assumptions section have not been violated. Therefore, the three steps required to run a paired t-test in Minitab are shown below:

1. Click Stat > Basic Statistics > Paired t... on the top menu, as shown below:
   

   Published with written permission from Minitab Inc.

   
   You will be presented with the following Paired t (Test and Confidence Interval) dialogue box:
   
   

   Published with written permission from Minitab Inc.

2. Leave the Samples in columns option selected. Then, enter one related group, Post, into the First sample: box, and the other related group, Pre, into the Second sample: box. You will end up with the dialogue box shown below:
   

   Published with written permission from Minitab Inc.

   Note 1: To transfer your variables, you first need to click into the First sample: box for your two related groups to appear in the main left-hand box (e.g., C1   Pre and C2   Post). 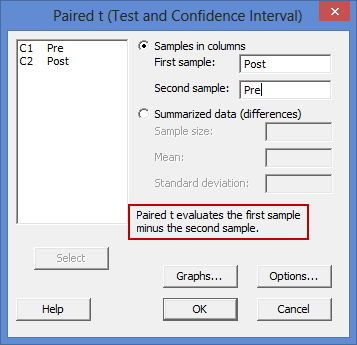To transfer the first related group, Post, into the First sample: box, you can now either select C2   Post in the main left-hand box and press the button or simply double-click on C2   Post (N.B., the button will be faded – – until you select one of your variables). You now need to do the same for C1   Pre, but this time into the Second sample: box.

   Explanation: You need to make sure that you enter your related groups into the correct boxes (i.e., the First sample: and Second sample: boxes). This is because in Minitab, the setup is such that the "Paired t evaluates the first sample minus the second sample", as highlighted in the red rectangle below:
   
   
   
   Therefore, if your two related groups are two "time points" (e.g., a pre-test post-test study design), as in our example of cigarette consumption before and after a hypnotherapy programme, you will typically subtract the scores on the dependent variable for the first time point from the scores for the second time point (e.g., the scores "before" an intervention has taken place are subtracted from the scores "after" the intervention). In such a case, the "second" time point acts as the First sample: and the "first" time point acts as the Second sample:.
   
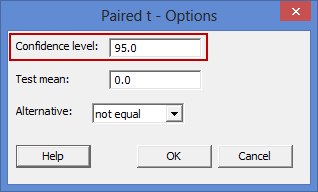
   Alternately, if you have a study design where you are interested in the differences between two "conditions" (see the assumption on related groups if you are unsure what this means), there will often be a control group and experimental group. In such a case, you will typically subtract the scores on the dependent variable for the control group from your experimental group (i.e., the experimental group minus the control group). In such a case, the "experimental group" acts as the First sample: and the "control group" acts as the Second sample:.

   Note 2: By default, Minitab uses 95% confidence intervals, which equates to declaring statistical significance at the p < .05 level. If you want to change this, you can do so by first clicking on the button, which opens the Paired t - Options dialogue box, as shown below:
   
   
   
   To change the value of the confidence interval, simply click into the Confidence level: box – highlighted in red above – and change the value (e.g., a value of 99.0 would equate to declaring statistical significance at the p < .01 level).

3. Click on the button. The output that Minitab produces is shown below.

Minitab

Interpreting the paired t-test output in Minitab

The Minitab output for the paired t-test is shown below. This output provides useful descriptive statistics for the two related groups that were compared, including the sample size, mean, standard deviation and standard error of the mean, as well as actual results from the paired t-test.

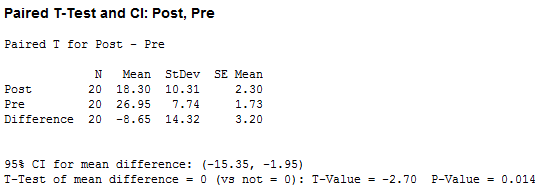
Looking at the "Mean" column, you can see that cigarette consumption amongst participants was lower after the hypnotherapy programme (18.30 cigarettes in the Post row) compared with before the hypnotherapy programme (26.95 cigarettes in the Pre row), with a mean difference between the two time periods of -8.65 cigarettes (shown in the Difference row). Also, when comparing the two time periods across the Difference row, we can see that the standard deviation was 14.32 cigarettes (the "StDev" column) with a standard error of the mean of 3.20 cigarettes (the "SE Mean" column). Furthermore, the 95% CI for mean difference row shows a 95% confidence interval (95% CI) for the mean difference of -15.35 to -1.95 cigarettes.

In the final row of Minitab output, you are presented with an obtained t-value (T-Value) of -2.70 and the statistical significance (2-tailed p-value) of the paired t-test (P-Value), which is 0.014. As the p-value is less than 0.05 (i.e., p < .05), it can be concluded that there is a statistically significant difference between the two time points (Pre and Post). In other words, the difference between mean cigarette consumption before and after the hypnotherapy programme is not equal to zero. Minitab does not include the degrees of freedom, but these are simply the sample size (the "N" column) minus 1 (i.e., N – 1). Therefore, in our example the degrees of freedom are 20 – 1, which is 19.

Note: In addition to the paired t-test output above, you will also have to interpret (a) the boxplots you created in Minitab to check if there were any significant outliers and (b) the output Minitab produces for your Shapiro-Wilk test of normality to determine normality (see the Assumptions section earlier if you are unsure what these assumptions are). Remember that if your data failed either of these assumptions, the output that you get from the paired t-test procedure (i.e., the output we discussed above) might not be valid and you will have to take steps to deal with such violations (e.g., transforming your data using Minitab) or use a different statistical test.

Minitab

Reporting the output of the paired t-test

When you report the output of your paired t-test, it is good practice to include:

• A. An introduction to the analysis you carried out.
• B. Information about your sample, including how many participants were in each group of your two related groups (N.B., this is particularly useful if the group sizes were unequal or there were missing values).
• C. A statement of whether there were statistically significant differences between your two related groups, including the relevant means (Mean) and standard deviations (StDev), mean difference (Difference), 95% confidence interval for the mean difference (95% CI for mean difference), t-value (T-Value), degrees of freedom, and significance level, or more specifically, the 2-tailed p-value (P-Value).

Based on the Minitab output above, we could report the results of this study as follows:

To make your results easier for others to understand, you can also produce a bar chart with error bars (e.g., where the errors bars could be the standard deviation, standard error or 95% confidence intervals). Furthermore, you are increasingly expected to report an "effect size" in addition to your paired t-test results. Effect sizes are important because whilst the paired t-test tells you whether differences between group means are "real" (i.e., different in the population), it does not tell you the "size" of the difference. Minitab does not automatically produce effect sizes through the paired t-test procedure, but there is a separate procedure in Minitab to do so.

Portions of information contained in this publication/book are printed with permission of Minitab Inc. All such material remains the exclusive property and copyright of Minitab Inc. All rights reserved.