Three-way ANOVA in Stata

Introduction

The three-way ANOVA is used to determine if there is an interaction effect between three independent variables on a continuous dependent variable (i.e., if a three-way interaction exists). As such, it extends the two-way ANOVA, which is used to determine if such an interaction exists between just two independent variables (i.e., rather than three independent variables).

Note: It is quite common for the independent variables to be called "factors" or "between-subjects factors", but we will continue to refer to them as independent variables in this guide. Furthermore, it is worth noting that the three-way ANOVA is also referred to more generally as a "factorial ANOVA" or more specifically as a "three-way between-subjects ANOVA".

A three-way ANOVA can be used in a number of situations. For example, you might be interested in the effect of two different types of exercise programme (i.e., type of exercise programme) for improving marathon running performance (i.e., time to run a marathon). However, you are concerned that the effect that each type of exercise programme has on marathon running performance might be different for males and females (i.e., depending on your gender), as well as if you are normal weight or obese (i.e., your body composition). Indeed, you suspect that the effect of the type of exercise programme on marathon running performance will depend on both your gender and body composition. As such, you want to determine if a three-way interaction effect exists between type of exercise programme, gender and body composition (i.e., the three independent variables) in explaining marathon running performance.

In this "quick start" guide, we show you how to carry out a three-way ANOVA using Stata, as well as interpret and report the results from this test. However, before we introduce you to this procedure, you need to understand the different assumptions that your data must meet in order for a three-way ANOVA to give you a valid result. We discuss these assumptions next.

Stata

Assumptions

There are six "assumptions" that underpin the three-way ANOVA. If any of these six assumptions are not met, you might not be able to analyze your data using a three-way ANOVA because you might not get a valid result. Since assumptions #1, #2 and #3 relate to your study design and choice of variables, they will not be tested using Stata. However, you should decide whether your study meets these assumptions before moving on.

• Assumption #1: Your dependent variable should be measured at the continuous level (i.e., it is an interval or ratio variable). Examples of such continuous variables include height (measured in feet and inches), temperature (measured in °C), salary (measured in US dollars), revision time (measured in hours), intelligence (measured using IQ score), reaction time (measured in milliseconds), test performance (measured from 0 to 100), sales (measured in number of transactions per month), and so forth. If you are unsure whether your dependent variable is continuous (i.e., measured at the interval or ratio level), see our Types of Variable guide.
• Assumption #2: Your three independent variables should each consist of two or more categorical, independent (unrelated) groups. Examples of categorical variables include gender (e.g., two groups: male and female), ethnicity (e.g., three groups: Caucasian, African American and Hispanic), profession (e.g., five groups: surgeon, doctor, nurse, dentist, therapist), and so forth.
• Assumption #3: You should have independence of observations, which means that there is no relationship between the observations in each group or between the groups themselves (technically, no relationship between the errors). For example, there must be different participants in each group with no participant being in more than one group. If you do not have independence of observations, it is likely you have "related groups", which means you might need to use a three-way mixed or repeated measures ANOVA instead of the three-way ANOVA.

Fortunately, you can check assumptions #4, #5 and #6 using Stata. When testing these assumptions, do not be surprised if your data fails one or more of them since this is fairly typical when working with real-world data rather than textbook examples, which often only show you how to carry out a three-way ANOVA when everything goes well. However, don’t worry because even when your data fails certain assumptions, there is often a solution to overcome this (e.g., transforming your data or using another statistical test instead). Just remember that if you do not check that your data meets these assumptions or you test for them incorrectly, the results you get when running a three-way ANOVA might not be valid.

• Assumption #4: There should be no significant outliers. An outlier is simply a single case within your data set that does not follow the usual pattern (e.g., in a study of 100 students' IQ scores, where the mean score was 108 with only a small variation between students, one student had a score of 156, which is very unusual, and may even put her in the top 1% of IQ scores globally). The problem with outliers is that they can have a negative effect on the three-way ANOVA, reducing the accuracy of your results. Fortunately, when using Stata to run a three-way ANOVA on your data, you can easily detect possible outliers.
• Assumption #5: Your dependent variable should be approximately normally distributed for each combination of the groups of the three independent variables. Your data need only be approximately normal for running a three-way ANOVA because it is somewhat "robust" to violations of normality, meaning that this assumption can be a little violated and still provide valid results. You can test for normality using the Shapiro-Wilk test of normality, which is easily tested for using Stata.
• Assumption #6: There needs to be homogeneity of variances for each combination of the groups of the three independent variables. You can test this assumption in Stata using Levene's test for homogeneity of variances.

Checking these assumptions is not a difficult task and Stata provides all the tools you need to do this.

In the section, Test Procedure in Stata, we illustrate the Stata procedure required to perform a three-way ANOVA assuming that no assumptions have been violated. First, we set out the example we use to explain the three-way ANOVA procedure in Stata.

Stata

Example

A researcher wanted to examine a new class of drug that has the potential to lower cholesterol levels and thus help against heart attack. Due to the specific molecular mechanisms by which this new class of drugs work, the researcher hypothesized that the new class of drug might affect males and females differently, as well as those those already at risk of a heart attack. There were three different types of drug within this new class of drug, but the researcher was unsure which would be more successful.

Therefore, the researcher recruited 72 participants split evenly between males and females. Males and females were further (equally) subdivided into whether they were at low or high risk of heart attack. Each of these subgroups then received one of the three different drugs. After one month on the different drugs, cholesterol concentration was measured. The researcher wants to understand how each factor (i.e., type of drug, risk of heart attack, gender) interact to predict cholesterol concentration.

Participants' cholesterol concentration was recorded in the variable cholesterol, their gender in gender, their risk of heart attack in risk and the drug they took in the variable drug. In variable terms, the researcher wants to know if there is an interaction between gender, risk and drug on cholesterol.

Note: The data in our example is made up to illustrate the use of the three-way ANOVA (i.e., the data is fictitious).

Stata

Setup in Stata

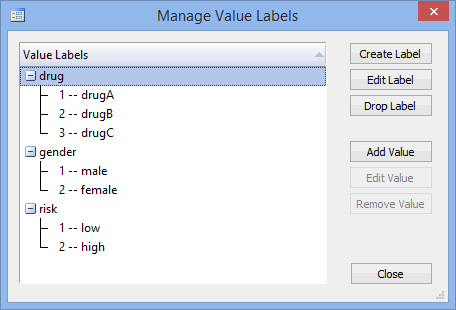
In Stata, we separated the individuals into their appropriate groups by using three columns representing the three independent variables, and labelled them gender, risk and drug. For gender, we coded "Male" as 1 and "Female" as 2; for risk, we coded "low" as 1and "high" as 2; and for drug, we coded "drugA" as 1, "drugB" as 2 and "drugC" as 3. The participants' cholesterol concentrations – the dependent variable – was entered under the variable name, cholesterol. The setup for this example can be seen below:

Published with written permission from StataCorp LP.

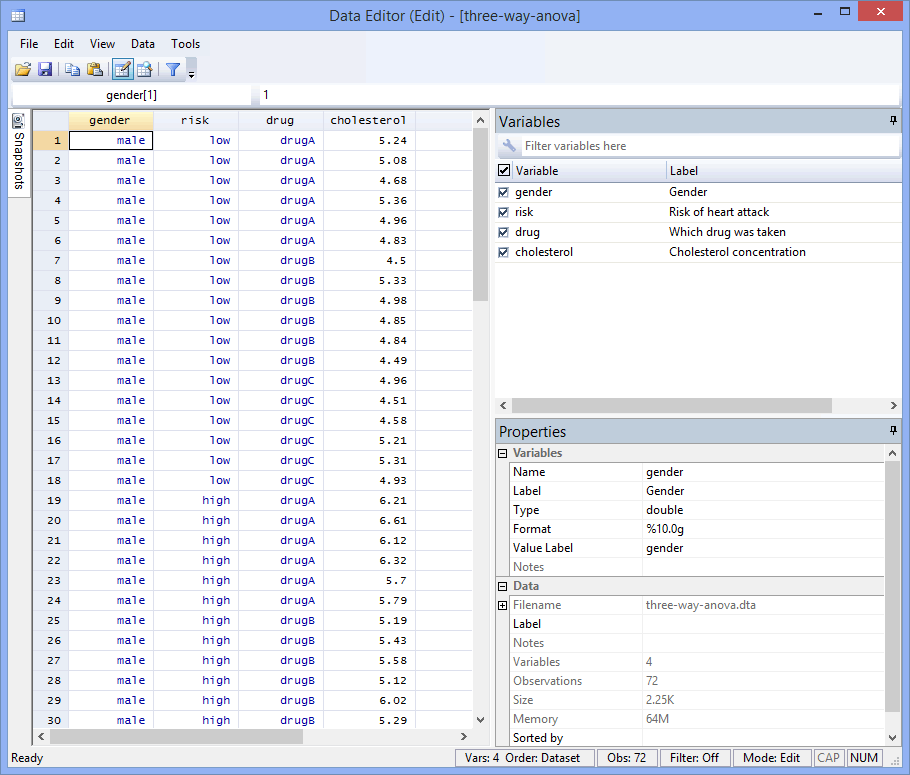
The scores for the independent variables – gender, risk and drug – as well as the scores for the dependent variable, cholesterol, were then entered into the Data Editor (Edit) spreadsheet, as shown below:

Published with written permission from StataCorp LP.

Stata

Test Procedure in Stata

In this section, we show you how to analyze your data using a three-way ANOVA in Stata when the six assumptions in the previous section, Assumptions, have not been violated. You can carry out a three-way ANOVA using code or Stata's graphical user interface (GUI). After you have carried out your analysis, we show you how to interpret your results. First, choose whether you want to use code or Stata's graphical user interface (GUI).

Stata

Code

In the first section below, we set out the code to carry out a three-way ANOVA. All code is entered into Stata's box, as illustrated below:

Published with written permission from StataCorp LP.

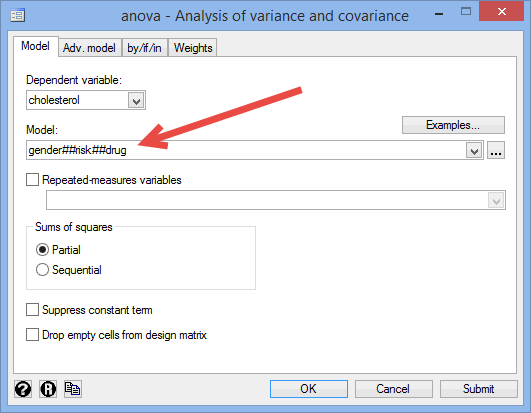
The code to run a three-way ANOVA on your data takes the form:

anova DependentVariable FirstIndependentVariable##SecondIndependentVariable##ThirdIndependentVariable

Using our example where the dependent variable is cholesterol and the three independent variables are gender, risk and drug, the required code would be:

anova cholesterol gender##risk##drug

Therefore, enter the code and press the "Return/Enter" key on your keyword.

You can see the Stata output that will be produced here. If there is a statistically significant interaction, you can carry out simple two-way interactions. We discuss this later.

Stata

Graphical user interface (GUI)

1. Click Statistics > Linear models and related > ANOVA/MANOVA > Analysis of variance and covariance on the top menu, as shown below:
   

   Published with written permission from StataCorp LP.

   
   You will be presented with the following anova - Analysis of variance and covariance dialogue box:
   
   

   Published with written permission from StataCorp LP.

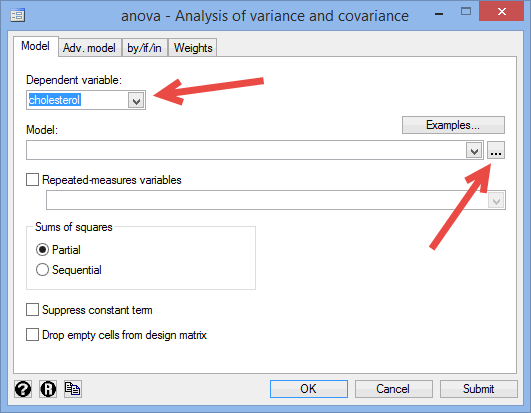
2. Select the dependent variable, cholesterol, from within the Dependent variable: drop-down box, and click on the three dot button, , to the far right of the Model: drop-down box, as shown below:
   

   Published with written permission from StataCorp LP.

   
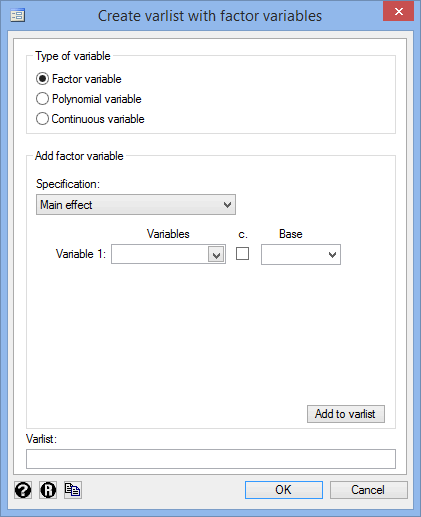
   You will be presented with the following Create varlist with factor variables dialogue box:
   
   

   Published with written permission from StataCorp LP.

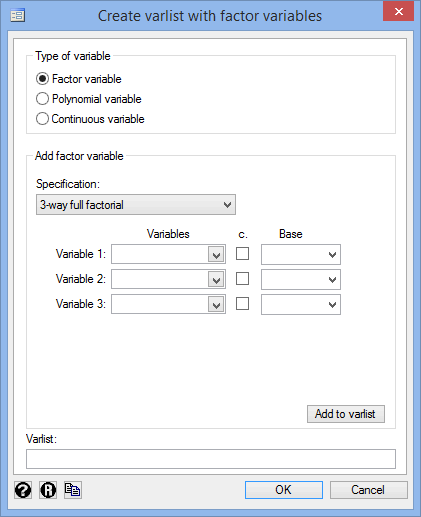
3. Keep the Factor variable option selected in the –Type of variable– area. In the –Add factor variable– area, select the option from within the Specification: drop-down box. You will be presented with two more Variables drop-down boxes, as shown below:
   

   Published with written permission from StataCorp LP.

4. For Variable 1:, select gender under the Variables drop-down box; for Variable 2:, select risk under the Variables drop-down box; and for Variable 3:, select drug under the Variables drop-down box. Then, click the button, which will add the Model term, gender##risk##drug, to the Varlist: box.
   

   Published with written permission from StataCorp LP.

   Note: We have not ticked the check box, , under c. for any of the three independent variables, gender, risk or drug. This is because Assumption #2 of a three-way ANOVA is that all independent variables are "factorial variables" (i.e., categorical variables).

5. Click on the button. You will be presented with the anova - Analysis of variance and covariance dialogue box, but now with the Model term, gender##risk##drug, having been added in the Model: box, as highlighted below:
   

   Published with written permission from StataCorp LP.

6. Click on the button. This will generate the Stata output for the three-way ANOVA, shown in the next section.

Stata

Output of the three-way ANOVA in Stata

If your data passed assumption #4 (i.e., there were no significant outliers), assumption #5 (i.e., your dependent variable was approximately normally distributed for each group combination of the independent variables) and assumption #6 (i.e., there was homogeneity of variances), which we explained earlier in the Assumptions section, you will only need to interpret the following Stata output for the three-way ANOVA:

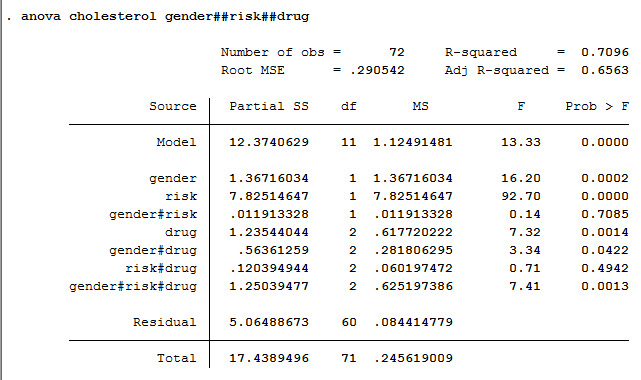
Published with written permission from StataCorp LP.

The row of greatest interest is the gender#risk#drug row because this contains the result of whether we have a statistically significant three-way interaction.

If we read across the gender#risk#drug row until we come to the Prob > F column, we are presented with the statistical significance level, which is p = .0013. We can, therefore, declare that we have a statistically significant three-way interaction.

Finally, if you have a statistically significant interaction, you will also need to run and report simple two-way interactions, as well as perhaps simple simple main effects and simple simple comparisons. Alternately, if you do not have a statistically significant interaction, you would consider the two-way interactions instead. All of these follow up analyses can be calculated using Stata.

Stata

Reporting the results of a three-way ANOVA

When you report the output of your three-way ANOVA, it is good practice to include:

• A. An introduction to the analysis you carried out.
• B. Information about your sample (including how many participants were in each of your groups if the group sizes were unequal or there were missing values).
• C. A statement of whether there was a statistically significant interaction between your three independent variables on the dependent variable (including the observed F-value [F], degrees of freedom [df], and significance level, or more specifically, the 2-tailed p-value [Prob > F].
• D. If the three-way interaction was statistically significant, follow up tests that might include simple two-way interactions, simple simple main effects and simple simple comparisons.

Based on the Stata output above, we could report the results of this study as follows: