Fleiss' kappa in SPSS Statistics
Introduction
Fleiss' kappa, κ (Fleiss, 1971; Fleiss et al., 2003), is a measure of inter-rater agreement used to determine the level of agreement between two or more raters (also known as "judges" or "observers") when the method of assessment, known as the response variable, is measured on a categorical scale. In addition, Fleiss' kappa is used when: (a) the targets being rated (e.g., patients in a medical practice, learners taking a driving test, customers in a shopping mall/centre, burgers in a fast food chain, boxes delivered by a delivery company, chocolate bars from an assembly line) are randomly selected from the population of interest rather than being specifically chosen; and (b) the raters who assess these targets are non-unique and are randomly selected from a larger population of raters. We explain these three concepts – random selection of targets, random selection of raters and non-unique raters – as well as the use of Fleiss' kappa in the example below.
As an example of how Fleiss' kappa can be used, imagine that the head of a large medical practice wants to determine whether doctors at the practice agree on when to prescribe a patient antibiotics. Therefore, four doctors were randomly selected from the population of all doctors at the large medical practice to examine a patient complaining of an illness that might require antibiotics (i.e., the "four randomly selected doctors" are the non-unique raters and the "patients" are the targets being assessed). The four randomly selected doctors had to decide whether to "prescribe antibiotics", "request the patient come in for a follow-up appointment" or "not prescribe antibiotics" (i.e., where "prescribe", "follow-up" and "not prescribe" are three categories of the nominal response variable, antibiotics prescription decision). This process was repeated for 10 patients, where on each occasion, four doctors were randomly selected from all doctors at the large medical practice to examine one of the 10 patients. The 10 patients were also randomly selected from the population of patients at the large medical practice (i.e., the "population" of patients at the large medical practice refers to all patients at the large medical practice). The level of agreement between the four non-unique doctors for each patient is analysed using Fleiss' kappa. Since the results showed a very good strength of agreement between the four non-unique doctors, the head of the large medical practice feels somewhat confident that doctors are prescribing antibiotics to patients in a similar manner. Furthermore, an analysis of the individual kappas can highlight any differences in the level of agreement between the four non-unique doctors for each category of the nominal response variable. For example, the individual kappas could show that the doctors were in greater agreement when the decision was to "prescribe" or "not prescribe", but in much less agreement when the decision was to "follow-up". It is also worth noting that even if raters strongly agree, this does not mean that their decision is correct (e.g., the doctors could be misdiagnosing the patients, perhaps prescribing antibiotics too often when it is not necessary). This is something that you have to take into account when reporting your findings, but it cannot be measured using Fleiss' kappa.
In this introductory guide to Fleiss' kappa, we first describe the basic requirements and assumptions of Fleiss' kappa. These are not things that you will test for statistically using SPSS Statistics, but you must check that your study design meets these basic requirements/assumptions. If your study design does not meet these basic requirements/assumptions, Fleiss' kappa is the incorrect statistical test to analyse your data. However, there are often other statistical tests that can be used instead. Next, we set out the example we use to illustrate how to carry out Fleiss' kappa using SPSS Statistics. This is followed by the Procedure section, where we illustrate the simple 6-step Reliability Analysis... procedure that is used to carry out Fleiss' kappa in SPSS Statistics. Next, we explain how to interpret the main results of Fleiss' kappa, including the kappa value, statistical significance and 95% confidence interval, which can be used to assess the agreement between your two or more non-unique raters. We also discuss how you can assess the individual kappas, which indicate the level of agreement between your two or more non-unique raters for each of the categories of your response variable (e.g., indicating that doctors were in greater agreement when the decision was the "prescribe" or "not prescribe", but in much less agreement when the decision was to "follow-up", as per our example above). In the final section, Reporting, we explain the information you should include when reporting your results. A Bibliography and Referencing section is included at the end for further reading. To continue with this introductory guide, go to the next section.
SPSS Statistics
Basic requirements and assumptions of Fleiss' kappa
Fleiss' kappa is just one of many statistical tests that can be used to assess the inter-rater agreement between two or more raters when the method of assessment (i.e., the response variable) is measured on a categorical scale (e.g., Scott, 1955; Cohen, 1960; Fleiss, 1971; Landis and Koch, 1977; Gwet, 2014). Each of these different statistical tests has basic requirements and assumptions that must be met in order for the test to give a valid/correct result. Fleiss' kappa is no exception. Therefore, you must make sure that your study design meets the basic requirements/assumptions of Fleiss' kappa. If your study design does not meet these basic requirements/assumptions, Fleiss' kappa is the incorrect statistical test to analyse your data. However, there are often other statistical tests that can be used instead. In this section, we set out six basic requirements/assumptions of Fleiss' kappa.
- Requirement/Assumption #1: The response variable that is being assessed by your two or more raters is a categorical variable. (i.e., you have an ordinal or nominal variable). A categorical variable can be either a nominal variable or an ordinal variable, but Fleiss' kappa does not take into account the ordered nature of an ordinal variable. Examples of nominal variables include gender (with two categories: "male" and "female"), ethnicity (with three categories: "African American", "Caucasian" and "Hispanic"), transport type (four categories: "cycle", "bus", "car" and "train"), and profession (five categories: "consultant", "doctor", "engineer", "pilot" and "scientist"). Examples of ordinal variables include educational level (e.g., with three categories: "high school", "college" and "university"), physical activity level (e.g., with four categories: "sedentary", "low", "moderate" and "high"), revision time (e.g., with five categories: "0-5 hours", "6-10 hours", "11-15 hours", "16-20 hours" and "21-25 hours"), Likert items (e.g., a 7-point scale from "strongly agree" through to "strongly disagree"), amongst other ways of ranking categories (e.g., a 5-point scale explaining how much a customer liked a product, ranging from "Not very much" to "Yes, a lot"). If these terms are unfamiliar to you, please see our guide on Types of Variable for further help.
For example, two raters could be assessing whether a patient's mole was "normal" or "suspicious" (i.e., two categories); four raters could be assessing whether the quality of service provided by a customer service agent was "above average", "average" or "below average" (i.e., three categories); or three raters could be assessing whether a person's physical activity level should be considered "sedentary", "low", "medium" or "high" (i.e., four categories). - Requirement/Assumption #2: The two or more categories of the response variable that are being assessed by the raters must be mutually exclusive, which has two components. First, the two or more categories are mutually exclusive because no categories can overlap. For example, a rater, such as a dermatologist (i.e., a skin specialist), could only consider a patient's mole to be "normal" or "suspicious". The mole cannot be "normal" and "suspicious" at the same time. Second, the two or more categories are mutually exclusive because only one category can be selected for each response. For example, when assessing the patient's mole, the dermatologist must judge the mole to be either "normal" or "suspicious". The dermatologist cannot select more than one category for each patient.
Note: If you have a study design where the categories of your response variable are not mutually exclusive, Fleiss' kappa is not the correct statistical test. If you would like us to let you know when we can add a guide to the site to help with this scenario, please contact us.
- Requirement/Assumption #3: The response variable that is being assessed must have the same number of categories for each rater. In other words, all the raters must use the same rating scale. For example, if one rater was asked to assess whether the quality of service provided by a customer service agent was "above average", "average" or "below average" (i.e., three categories), a second rater cannot only be given two options: "above average" and "below average" (i.e., two categories).
Note: If you have a study design where each response variable does not have the same number of categories, Fleiss' kappa is not the correct statistical test. If you would like us to let you know when we can add a guide to the site to help with this scenario, please contact us.
- Requirement/Assumption #4: The two or more raters are non-unique. As Fleiss et al. (2003, pp. 610-611) state: "The raters responsible for rating one subject are not assumed to be the same as those responsible for rating another".
To understand this further, as well as the difference between non-unique and unique raters, imagine a study where a large health organisation wants to determine the extent to which radiographers agree on the severity of a type of back injury, where severity is assessed on a scale from "Grade I" (the most severe), through to "Grade II", "Grade III" and "Grade IV" (the least severe). To assess severity, radiographers look at magnetic resonance imaging (MRI) slides that have been taken of the patient's back and are asked to make a judgement about whether the patient's back injury severity is "Grade I", "Grade II", "Grade III" or "Grade IV" (i.e., the four categories of the ordinal variable, "Back Injury Severity").
Now, imagine that in this study the large health organisation wants to determine the extent to which five radiographers (i.e., five raters) agree on the severity of back pain injuries. Furthermore, a total of 20 MRI slides are used (i.e., one MRI slide shows the back injury for one patient). Also, the radiographers who take part in the study are randomly selected from all 50 radiographers in the large health organisation (i.e., the total population of radiographers in the organisation). If the same five radiographers assessed all 20 MRI slides, these five radiographers would be described as unique raters. However, if a different set/group of radiographers rated each of the 20 MRI slides, these five radiographers would be described as non-unique raters (i.e., five randomly selected radiographers out of the 50 radiographers in the large organisation view and rate the first MRI slide, then another five randomly selected radiographers rate the second MRI slide, and so on, until all 20 MRI slides have been rated). Fleiss' kappa measures the level of agreement between non-unique raters.Note 1: As we mentioned above, Fleiss et al. (2003, pp. 610-11) stated that "the raters responsible for rating one subject are not assumed to be the same as those responsible for rating another". In this sense, there is no assumption that the five radiographers who rate one MRI slide are the same radiographers who rate another MRI slide. However, even though the five radiographers are randomly sampled from all 50 radiographers at the large health organisation, it is possible that some of the radiographers will be selected to rate more than one of the 20 MRI slides.
Note 2: If you have a study design where the two or more raters are not non-unique (i.e., they are unique), Fleiss' kappa is not the correct statistical test. If you would like us to let you know when we can add a guide to the site to help with this scenario, please contact us.
- Requirement/Assumption #5: The two or more raters are independent, which means that one rater's judgement does not affect another rater's judgement. For example, if the radiographers in the example above discuss their assessment of the MRI slides before recording their response or perhaps are simply in the same room when they make their assessment, this could influence the assessment they make. It is important that the potential for such bias is removed from the study design as much as possible.
- Requirement/Assumption #6: The targets being rated (e.g., patients in a medical practice, learners taking a driving test, customers in a shopping mall/centre, burgers in a fast food chain, boxes delivered by a delivery company, chocolate bars from an assembly line) ) are randomly selected from the population of interest rather than being specifically chosen.
For example, the randomly selected, non-unique radiographers in the example above rated 20 MRI slides. These 20 MRI slides were randomly selected from all MRI slides of patients' backs at the large health organisation (i.e., this is the total population of MRI slides from which the 20 MRI slides are randomly selected). The MRI slides from which 20 were selected were all of the same type. This is important because if some of MRI slides were taken with the latest equipment, whilst other MRI slides were taken with old equipment where the image was less clear, this will introduce bias. As another example, consider our first example of four randomly selected doctors in a large medical practice who assessed whether 10 patients should be prescribed antibiotics. These 10 patients had to be randomly selected from the total population of patients at the large medical practice (i.e., the "population" of patients at the large medical practice refers to all patients at the large medical practice).Note: If you have a study design where the targets being rated are not randomly selected, Fleiss' kappa is not the correct statistical test. If you would like us to let you know when we can add a guide to the site to help with this scenario, please contact us.
Therefore, before carrying out a Fleiss' kappa analysis, it is critical that you first check whether your study design meets these six basic requirements/assumptions. If your study design does not met requirements/assumptions #1 (i.e., you have a categorical response variable), #2 (i.e., the two or more categories of this response variable are mutually exclusive), #3 (i.e., the same number of categories are assessed by each rater), #4 (i.e., the two or more raters are non-unique), #5 (i.e., the two or more raters are independent), and #6 (i.e., targets are randomly sample from the population), Fleiss' kappa is the incorrect statistical test to analyse your data.
When you are confident that your study design has met all six basic requirements/assumptions described above, you can carry out a Fleiss' kappa analysis. In the sections that follow we show you how to do this using SPSS Statistics, based on the example we set out in the next section: Example used in this guide.
SPSS Statistics
Example used in this guide
A local police force wanted to determine whether police officers with a similar level of experience were able to detect whether the behaviour of people in a clothing retail store was "normal", "unusual, but not suspicious" or "suspicious". In particular, the police force wanted to know the extent to which its police officers agreed in their assessment of individuals' behaviour fitting into one of these three categories (i.e., where the three categories were "normal", "unusual, but not suspicious" or "suspicious" behaviour). In other words, the police force wanted to assess police officers' level of agreement.
To assess police officers' level of agreement, the police force conducted an experiment where three police officers were randomly selected from all available police officers at the local police force of approximately 100 police officers. These three police offers were asked to view a video clip of a person in a clothing retail store (i.e., the people being viewed in the clothing retail store are the targets that are being rated). This video clip captured the movement of just one individual from the moment that they entered the retail store to the moment they exited the store. At the end of the video clip, each of the three police officers was asked to record (i.e., rate) whether they considered the person’s behaviour to be "normal", "unusual, but not suspicious" or "suspicious" (i.e., where these are three categories of the nominal response variable, behavioural_assessment). Since there must be independence of observations, which is one of the assumptions/basic requirements of Fleiss' kappa, as explained earlier, each police officer rated the video clip in a room where they could not influence the decision of the other police officers to avoid possible bias.
This process was repeated for a total of 23 video clips where: (a) each video clip was different; and (b) a new set of three police officers were randomly selected from all 100 police officers each time (i.e., three police officers were randomly selected to assess video clip #1, another three police officers were randomly selected to assess video clip #2, another three police officers were randomly selected to assess video clip #3, and so forth, until all 23 video clips had been rated). Therefore, the police officers were considered non-unique raters, which is one of the assumptions/basic requirements of Fleiss' kappa, as explained earlier. After all of the 23 video clips had been rated, Fleiss' kappa was used to compare the ratings of the police officers (i.e., to compare police officers' level of agreement).
Note: Please note that this is a fictitious study being used to illustrate how to carry out and interpret Fleiss' kappa.
SPSS Statistics
SPSS Statistics procedure to carry out a Fleiss' kappa analysis
The procedure to carry out Fleiss' kappa, including individual kappas, is different depending on whether you have versions 26 to 30 (or the subscription version of SPSS Statistics) compared to version 25 or earlier versions of SPSS Statistics. The latest versions of SPSS Statistics are version 30 and the subscription version. If you are unsure which version of SPSS Statistics you are using, see our guide: Identifying your version of SPSS Statistics.
In this section, we show you how to carry out Fleiss' kappa using the 6-step Reliability Analysis... procedure in SPSS Statistics, which is a "built-in" procedure that you can use if you have SPSS Statistics versions 26 to 30 (or the subscription version of SPSS Statistics). If you have SPSS Statistics version 25 or an earlier version of SPSS Statistics, please see the Note below:
Note: If you have SPSS Statistics version 25 or an earlier version of SPSS Statistics, you cannot use the Reliability Analysis... procedure. However, you can use the FLEISS KAPPA procedure, which is a simple 3-step procedure. Unfortunately, FLEISS KAPPA is not a built-in procedure in SPSS Statistics, so you need to first download this program as an "extension" using the Extension Hub in SPSS Statistics. You can then run the FLEISS KAPPA procedure using SPSS Statistics.
Therefore, if you have SPSS Statistics version 25 or an earlier version of SPSS Statistics, our enhanced guide on Fleiss' kappa in the members' section of Laerd Statistics includes a page dedicated to showing how to download the FLEISS KAPPA extension from the Extension Hub in SPSS Statistics and then carry out a Fleiss' kappa analysis using the FLEISS KAPPA procedure. You can access this enhanced guide by subscribing to Laerd Statistics.
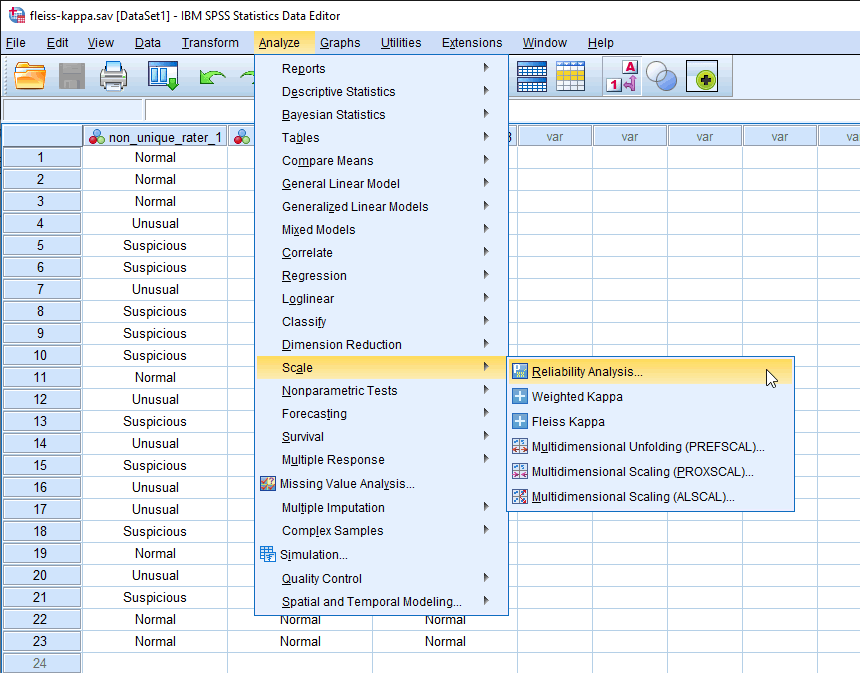
- Click Analyze > Scale > Reliability Analysis... on the top menu, as shown below:
Note: In version 27 and the subscription version, SPSS Statistics introduced a new look to their interface called "SPSS Light", replacing the previous look for versions 26 and earlier versions, which was called "SPSS Standard". Therefore, if you have SPSS Statistics versions 27 to 30 (or the subscription version of SPSS Statistics), the images that follow will be light grey rather than blue. However, the procedure is identical in SPSS Statistics versions 26 to 30 (and the subscription version of SPSS Statistics).

Published with written permission from SPSS Statistics, IBM Corporation.
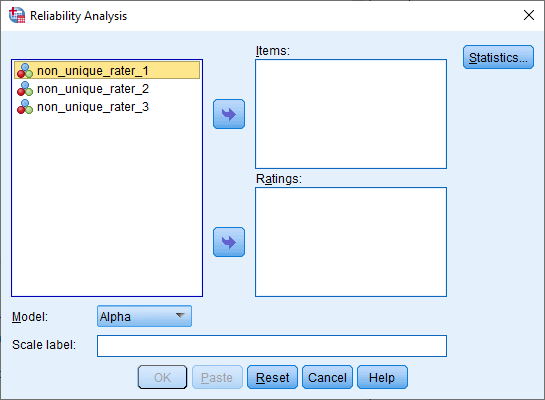
You will be presented with the following Reliability Analysis dialogue box:

Published with written permission from SPSS Statistics, IBM Corporation.
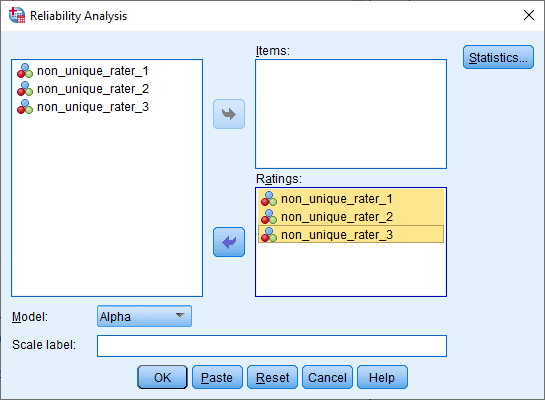
- Transfer your two or more variables, which in our example are non_unique_rater_1, non_unique_rater_2 and non_unique_rater_3, into the Ratings: box, using the bottom
 button. You will end up with a screen similar to the one below:
button. You will end up with a screen similar to the one below:
Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
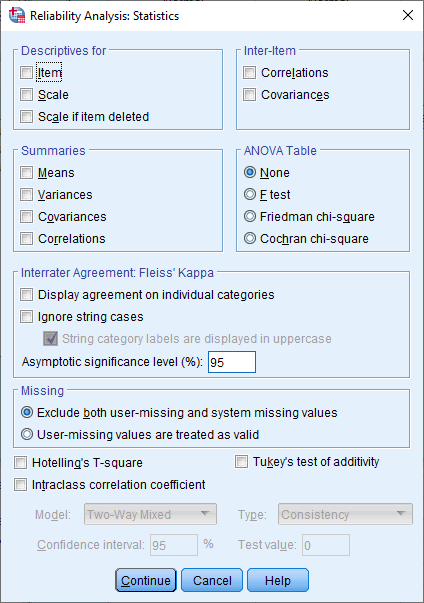
 button. You will be presented with the Reliability Analysis: Statistics dialogue box, as shown below:
button. You will be presented with the Reliability Analysis: Statistics dialogue box, as shown below:
Published with written permission from SPSS Statistics, IBM Corporation.
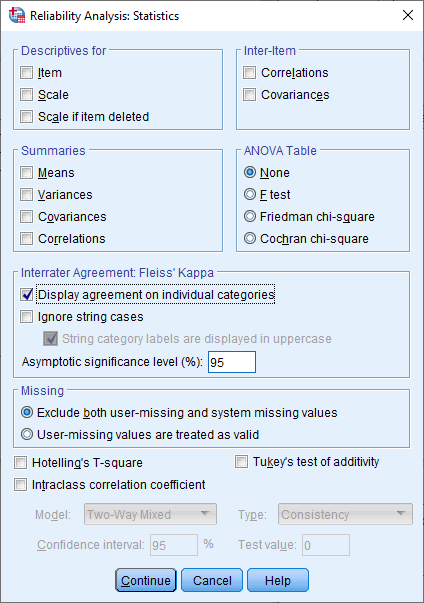
- Select the Display agreement on individual categories option in the –Interrater Agreement: Fleiss' Kappa– area, as shown below:

Published with written permission from SPSS Statistics, IBM Corporation.
- Click on the
 button. This will return you to the Reliability Analysis... dialogue box.
button. This will return you to the Reliability Analysis... dialogue box. - Click on the
 button to generate the output for Fleiss' kappa.
button to generate the output for Fleiss' kappa.
Now that you have run the Reliability Analysis... procedure, we show you how to interpret the results from a Fleiss' kappa analysis in the next section.
SPSS Statistics
Interpreting the results from a Fleiss' kappa analysis
Fleiss' kappa (κ) is a statistic that was designed to take into account chance agreement. In terms of our example, even if the police officers were to guess randomly about each individual's behaviour, they would end up agreeing on some individual's behaviour simply by chance. However, you do not want this chance agreement affecting your results (i.e., making agreement appear better than it actually is). Therefore, instead of measuring the overall proportion of agreement, Fleiss' kappa measures the proportion of agreement over and above the agreement expected by chance (i.e., over and above chance agreement).
After carrying out the Reliability Analysis... procedure in the previous section, the following Overall Kappa table will be displayed in the IBM SPSS Statistics Viewer, which includes the value of Fleiss' kappa and other associated statistics:

Published with written permission from SPSS Statistics, IBM Corporation.
The value of Fleiss' kappa is found under the "Kappa" column of the table, as highlighted below:

Published with written permission from SPSS Statistics, IBM Corporation.
You can see that Fleiss' kappa is .557. This is the proportion of agreement over and above chance agreement. Fleiss' kappa can range from -1 to +1. A negative value for kappa (κ) indicates that agreement between the two or more raters was less than the agreement expected by chance, with -1 indicating that there was no observed agreement (i.e., the raters did not agree on anything), and 0 (zero) indicating that agreement was no better than chance. However, negative values rarely actually occur (Agresti, 2013). Alternately, kappa values increasingly greater that 0 (zero) represent increasing better-than-chance agreement for the two or more raters, to a maximum value of +1, which indicates perfect agreement (i.e., the raters agreed on everything).
There are no rules of thumb to assess how good our kappa value of .557 is (i.e., how strong the level of agreement is between the police officers). With that being said, the following classifications have been suggested for assessing how good the strength of agreement is when based on the value of Cohen's kappa coefficient. The guidelines below are from Altman (1999), and adapted from Landis and Koch (1977):
| Value of κ | Strength of agreement |
|---|---|
| < 0.20 | Poor |
| 0.21-0.40 | Fair |
| 0.41-0.60 | Moderate |
| 0.61-0.80 | Good |
| 0.81-1.00 | Very good |
| Table: Classification of Cohen's kappa. | |
Using this classification scale, since Fleiss' kappa (κ)=.557, this represents a moderate strength of agreement. However, the value of kappa is heavily dependent on the marginal distributions, which are used to calculate the level (i.e., proportion) of chance agreement. As such, the value of kappa will differ depending on the marginal distributions. This is one of the greatest weaknesses of Fleiss' kappa. It means that you cannot compare one Fleiss' kappa to another unless the marginal distributions are the same.
It is also good to report a 95% confidence interval for Fleiss' kappa. To do this, you need to consult the "Lower 95% Asymptotic CI Bound" and the "Upper 95% Asymptotic CI Bound" columns, as highlighted below:

Published with written permission from SPSS Statistics, IBM Corporation.
You can see that the 95% confidence interval for Fleiss' kappa is .389 to .725. In other words, we can be 95% confident that the true population value of Fleiss' kappa is between .389 and .725.
We can also report whether Fleiss' kappa is statistically significant; that is, whether Fleiss' kappa is different from 0 (zero) in the population (sometimes described as being statistically significantly different from zero). These results can be found under the "Z" and "P Value" columns, as highlighted below:

Published with written permission from SPSS Statistics, IBM Corporation.
You can see that the p-value is report as .000, which means that p < .0005 (i.e., the p-value is less than .0005). If p < .05 (i.e., if the p-value is less than .05), you have a statistically significant result and your Fleiss' kappa coefficient is statistically significantly different from 0 (zero). If p > .05 (i.e., if the p-value is greater than .05), you do not have a statistically significant result and your Fleiss' kappa coefficient is not statistically significantly different from 0 (zero). In our example, p =.000, which actually means p < .0005 (see the note below). Since a p-value less than .0005 is less than .05, our kappa (κ) coefficient is statistically significantly different from 0 (zero).
Note: If you see SPSS Statistics state that the "P Value" is ".000", this actually means that p < .0005; it does not mean that the significance level is actually zero. Where possible, it is preferable to state the actual p-value rather than a greater/less than p-value statement (e.g., p =.023 rather than p < .05, or p =.092 rather than p > .05). This way, you convey more information to the reader about the level of statistical significance of your result.
However, it is important to mention that because agreement will rarely be only as good as chance agreement, the statistical significance of Fleiss' kappa is less important than reporting a 95% confidence interval.
Therefore, we know so far that there was moderate agreement between the officers' judgement, with a kappa value of .557 and a 95% confidence interval (CI) between .389 and .725. We also know that Fleiss' kappa coefficient was statistically significant. However, we can go one step further by interpreting the individual kappas.
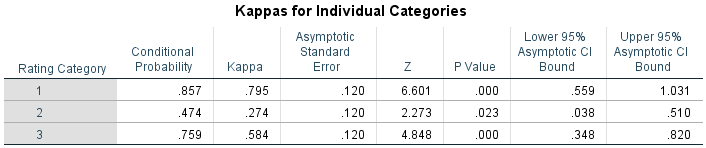
The individual kappas are simply Fleiss' kappa calculated for each of the categories of the response variable separately against all other categories combined. In our example, the following comparisons would be made:
- A. The "Normal" behaviour category would be compared to the "Unusual, but not suspicious" behaviour category and the "Suspicious" behaviour category combined.
- B. The "Unusual, but not suspicious" behaviour category would be compared to the "Normal" behaviour category and the "Suspicious" behaviour category combined.
- C. The "Suspicious" behaviour category would be compared to the "Normal" behaviour category and the "Unusual, but not suspicious" behaviour category combined.
We can use this information to assess police officers' level of agreement when rating each category of the response variable. For example, these individual kappas indicate that police officers are in better agreement when categorising individual's behaviour as either normal or suspicious, but far less in agreement over who should be categorised as having unusual, but not suspicious behaviour. These individual kappa results are displayed in the Kappas for Individual Categories table, as shown below:
Published with written permission from SPSS Statistics, IBM Corporation.
If you are unsure how to interpret the results in the Kappas for Individual Categories table, our enhanced guide on Fleiss' kappa in the members' section of Laerd Statistics includes a section dedicated to explaining how to interpret these individual kappas. You can access this enhanced guide by subscribing to Laerd Statistics. However, to continue with this introductory guide, go to the next section where we explain how to report the results from a Fleiss' kappa analysis.
SPSS Statistics
Reporting the results from a Fleiss' kappa analysis
When you report the results of a Fleiss' kappa analysis, it is good practice to include the following information:
- A. An introduction to the analysis you carried out, which includes: (a) the statistical test being used to analyse your data (i.e., Fleiss' kappa); (b) the raters whose level of agreement is being assessed (e.g., police officers in our example); (c) the targets who are being rated (e.g., individuals in a clothing retail store in our example); and (d) the categories of your response variable (e.g., the "Normal", "Unusual, but not suspicious", and "Suspicious" categories in our example), to highlight that the response variable is a categorical variable, as discussed in Requirement/Assumption #1.
- B. Information about your sample, including: (a) the number of non-unique raters and the population from which these were randomly selected; and (b) the number of targets and the population from which these were randomly selected. Including terms such as non-unique and randomly selected indicates to the reader that Fleiss' kappa has been used appropriately, as per Requirement/Assumption #4 and Requirement/Assumption #6 respectively.
- C. A statement to indicate how you helped to ensure independence of observations in order to reduce potential bias, as discussed in Requirement/Assumption #5.
- D. A statement to indicate that: (a) each rater was presented with the same number of categories; and (b) the categories were mutually exclusive, as per Requirement/Assumption #3 and Requirement/Assumption #2 respectively.
- E. The results from the Fleiss' kappa analysis, including: (a) the Fleiss' kappa coefficient, κ (i.e., shown under the "Kappa" column in the Overall Kappa table), together with the 95% confidence interval (CI) (i.e., shown under the "Lower 95% Asymptotic CI Bound" and the "Upper 95% Asymptotic CI Bound" columns); and (b) the p-value given for the test (i.e., shown under the "P Value" column). You can also consider including (c), the level of agreement in terms of a general guideline, such as the classifications of "poor", "fair", "moderate", "good" or "very good" agreement, suggested by Altman (1999) for the Cohen's kappa coefficient, and adapted from Landis and Koch (1977).
- F. The results from the individual kappa analysis, including: (a) the Fleiss' kappa coefficient, κ, for each category of the response variable separately against all other categories combined; and (b) a statement of the relative level of agreement between raters for each category.
- G. A table of your results, showing how the raters scored for each category of the response variable, assuming that data is anonymous and meets other relevant ethical standards of care. Providing such a table is important, where possible, because it allows others to: (a) check that you have carried out your analysis correctly; and (b) analyse your data using alternative methods of inter-rater agreement.
In the example below, we show how to report the results from your Fleiss' kappa analysis in line with five of the seven reporting guidelines above (i.e., A, B, C, D and E). If you are interested in understanding how to report your results in line with the two remaining reporting guidelines (i.e., F, in terms of individual kappas, and G, using a table), we show you how to do this in our enhanced guide on Fleiss' kappa in the members' section of Laerd Statistics. You can access this enhanced guide by subscribing to Laerd Statistics. However, if you are simply interested in reporting guidelines A to E, see the reporting example below:
- General
Fleiss' kappa was run to determine if there was agreement between police officers' judgement on whether 23 individuals in a clothing retail store were exhibiting either normal, unusual but not suspicious, or suspicious behaviour, based on a video clip showing each shopper's movement through the clothing retail store. Three non-unique police officers were chosen at random from a group of 100 police officers to rate each individual. Each police officer rated the video clip in a separate room so they could not influence the decision of the other police officers. When assessing an individual's behaviour in the clothing retail store, each police officer could select from only one of the three categories: "normal", "unusual but not suspicious" or "suspicious behaviour". The 23 individuals were randomly selected from all shoppers visiting the clothing retail store during a one-week period. Fleiss' kappa showed that there was moderate agreement between the officers' judgements, κ=.557 (95% CI, .389 to .725), p < .0005.
Note: When you report your results, you may not always include all seven reporting guidelines mentioned above (i.e., A, B, C, D, E, F and G) in the "Results" section, whether this is for an assignment, dissertation/thesis or journal/clinical publication. Some of the seven reporting guidelines may be included in the "Results" section, whilst others may be included in the "Methods/Study Design" section. However, we would recommend that all seven are included in at least one of these sections.
SPSS Statistics
Bibliography and Referencing
Please see the list below:
| Book | Agresti, A. (2013). Categorical data analysis (3rd ed.). Hoboken, NJ: John Wiley & Sons. |
| Book | Altman, D. G. (1999). Practical statistics for medical research. New York: Chapman & Hall/CRC Press. |
| Journal Article | Artstein, R., & Poesio, M. (2008). Inter-coder agreement for computational linguistics. Computational Linguistic, 34(4), 555-596. |
| Journal Article | Cohen, J. (1960). A coefficient of agreement for nominal scales. Educational and Psychological Measurement, 20, 37-46. |
| Journal Article | Di Eugenio, B., & Glass, M. (2004). The kappa statistic: A second look. Computational Statistics, 30(1), 95-101. |
| Journal | Fleiss, J. L. (1971). Measuring nominal scale agreement among many raters. Psychological Bulletin, 76, 378-382. |
| Book | Fleiss, J. L., Levin, B., & Paik, M. C. (2003). Statistical methods for rates and proportions (3rd ed.). Hoboken, NJ: Wiley. |
| Book | Gwet, K. L. (2014). Handbook of inter-rater reliability (4th ed.). Gaithersburg, MD: Advanced Analytics. |
| Journal Article | Landis, J. R., & Koch, G. G. (1977). The measurement of observer agreement for categorical data. Biometrics, 33, 159-174. |
| Journal Article | Scott, W. A. (1955). Reliability of content analysis: The case of nominal scale coding. Public Opinion Quarterly, 19, 321-325. |
| Book | Sheskin, D. J. (2011). Handbook of parametric and nonparametric statistical procedures (5th ed.). Boca Raton, FL: Chapman & Hall/CRC Press. |
SPSS Statistics
Reference this article
Laerd Statistics (2019). Fleiss' kappa using SPSS Statistics. Statistical tutorials and software guides. Retrieved Month, Day, Year, from https://statistics.laerd.com/spss-tutorials/fleiss-kappa-in-spss-statistics.php
For example, if you viewed this guide on 19th October 2019, you would use the following reference:
Laerd Statistics (2019). Fleiss' kappa using SPSS Statistics. Statistical tutorials and software guides. Retrieved October, 19, 2019, from https://statistics.laerd.com/spss-tutorials/fleiss-kappa-in-spss-statistics.php